2435. Paths in Matrix Whose Sum Is Divisible by K

Problem

You are given a 0-indexed m x n integer matrix grid and an integer k. You are currently at position (0, 0) and you want to reach position (m - 1, n - 1) moving only down or right.

Return** the number of paths where the sum of the elements on the path is divisible by **k. Since the answer may be very large, return it *modulo* 10^9 + 7.

  Example 1:

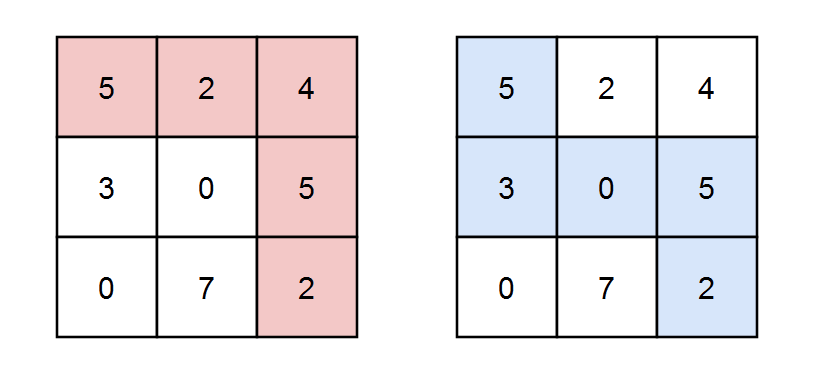
Input: grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
Output: 2
Explanation: There are two paths where the sum of the elements on the path is divisible by k.
The first path highlighted in red has a sum of 5 + 2 + 4 + 5 + 2 = 18 which is divisible by 3.
The second path highlighted in blue has a sum of 5 + 3 + 0 + 5 + 2 = 15 which is divisible by 3.

Example 2:

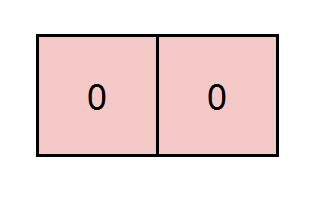
Input: grid = [[0,0]], k = 5
Output: 1
Explanation: The path highlighted in red has a sum of 0 + 0 = 0 which is divisible by 5.

Example 3:

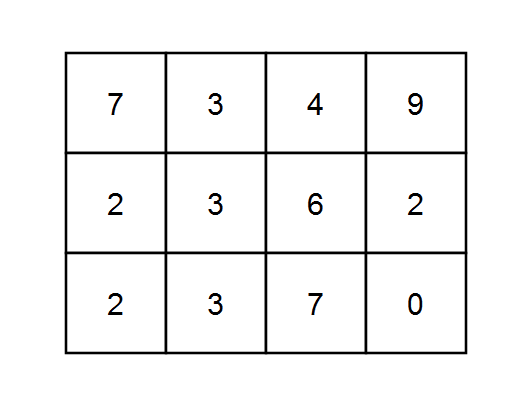
Input: grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
Output: 10
Explanation: Every integer is divisible by 1 so the sum of the elements on every possible path is divisible by k.

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 5 * 10^4

• 1 <= m * n <= 5 * 10^4

• 0 <= grid[i][j] <= 100

• 1 <= k <= 50

Solution (Java)

class Solution {
    int[][][] dp;
    int mod = 1_000_000_007;

    public int numberOfPaths(int[][] grid, int k) {
        int rows = grid.length;
        int cols = grid[0].length;
        dp = new int[rows][cols][k];
        for(int[][] a : dp) {
            for(int[] b : a) {
                Arrays.fill(b, -1);
            }
        }

        return helper(grid, 0, 0, 0, k);
    }

    int helper(int[][] grid, int r, int c, int sum, int k) {
        if(r < 0 || r == grid.length || c < 0 || c == grid[0].length) {
            return 0;
        }

        sum += grid[r][c];
        if(r == grid.length-1 && c == grid[0].length-1) {
            return sum%k==0 ? 1 : 0;
        }

        if(dp[r][c][sum%k] != -1) {
            return dp[r][c][sum%k];
        }

        dp[r][c][sum%k] = (helper(grid, r+1, c, sum, k) + helper(grid, r, c+1, sum, k)) % mod;
        return dp[r][c][sum%k];
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).