2328. Number of Increasing Paths in a Grid

Problem

You are given an m x n integer matrix grid, where you can move from a cell to any adjacent cell in all 4 directions.

Return **the number of *strictly* increasing paths in the grid such that you can start from any cell and end at any cell. **Since the answer may be very large, return it *modulo* 10^9 + 7.

Two paths are considered different if they do not have exactly the same sequence of visited cells.

  Example 1:

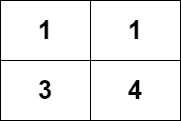
Input: grid = [[1,1],[3,4]]
Output: 8
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [1], [3], [4].
- Paths with length 2: [1 -> 3], [1 -> 4], [3 -> 4].
- Paths with length 3: [1 -> 3 -> 4].
The total number of paths is 4 + 3 + 1 = 8.

Example 2:

Input: grid = [[1],[2]]
Output: 3
Explanation: The strictly increasing paths are:
- Paths with length 1: [1], [2].
- Paths with length 2: [1 -> 2].
The total number of paths is 2 + 1 = 3.

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 1000

• 1 <= m * n <= 10^5

• 1 <= grid[i][j] <= 10^5

Solution

class Solution {
    private int help(int[][] a, int i, int j, int n, int m, int[][] dp) {
        if (i < 0 || i >= n || j >= m || j < 0) {
            return 0;
        }
        if (dp[i][j] != 0) {
            return dp[i][j];
        }
        long res = 0;
        if (i < n - 1 && a[i + 1][j] > a[i][j]) {
            res += 1 + help(a, i + 1, j, n, m, dp);
        }
        if (i > 0 && a[i - 1][j] > a[i][j]) {
            res += 1 + help(a, i - 1, j, n, m, dp);
        }
        if (j > 0 && a[i][j - 1] > a[i][j]) {
            res += 1 + help(a, i, j - 1, n, m, dp);
        }
        if (j < m - 1 && a[i][j + 1] > a[i][j]) {
            res += 1 + help(a, i, j + 1, n, m, dp);
        }
        dp[i][j] = (int) res % 1000000007;
        return dp[i][j];
    }

    public int countPaths(int[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        long ans = (long) n * m;
        int[][] dp = new int[n][m];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                ans += help(grid, i, j, n, m, dp) % 1000000007;
            }
        }
        ans = ans % 1000000007;
        return (int) ans;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).