2090. K Radius Subarray Averages

Problem

You are given a 0-indexed array nums of n integers, and an integer k.

The k-radius average for a subarray of nums centered at some index i with the radius k is the average of all elements in nums between the indices i - k and i + k (inclusive). If there are less than k elements before or after the index i, then the k-radius average is -1.

Build and return **an array *avgs* of length n where avgs[i] is the k-radius average for the subarray centered at index **i.

The average of x elements is the sum of the x elements divided by x, using integer division. The integer division truncates toward zero, which means losing its fractional part.

• For example, the average of four elements 2, 3, 1, and 5 is (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75, which truncates to 2.

  Example 1:

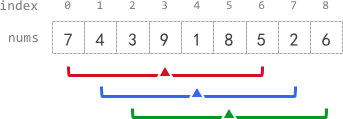
Input: nums = [7,4,3,9,1,8,5,2,6], k = 3
Output: [-1,-1,-1,5,4,4,-1,-1,-1]
Explanation:
- avg[0], avg[1], and avg[2] are -1 because there are less than k elements before each index.
- The sum of the subarray centered at index 3 with radius 3 is: 7 + 4 + 3 + 9 + 1 + 8 + 5 = 37.
  Using integer division, avg[3] = 37 / 7 = 5.
- For the subarray centered at index 4, avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4.
- For the subarray centered at index 5, avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4.
- avg[6], avg[7], and avg[8] are -1 because there are less than k elements after each index.

Example 2:

Input: nums = [100000], k = 0
Output: [100000]
Explanation:
- The sum of the subarray centered at index 0 with radius 0 is: 100000.
  avg[0] = 100000 / 1 = 100000.

Example 3:

Input: nums = [8], k = 100000
Output: [-1]
Explanation: 
- avg[0] is -1 because there are less than k elements before and after index 0.

  Constraints:

• n == nums.length

• 1 <= n <= 10^5

• 0 <= nums[i], k <= 10^5

Solution (Java)

class Solution {
    public int[] getAverages(int[] nums, int k) {
        // initialize result array with -1
        int[] res = new int[nums.length];
        Arrays.fill(res, -1);
        if (nums.length <= (k * 2)) {
            // return if not enough elements
            return res;
        }
        long sum = 0;
        long range = 2 * k + 1L;
        // take sum of all elements from 0 to k*2 index
        for (int i = 0; i <= 2 * k; ++i) {
            sum += nums[i];
        }
        // update first valid avg
        res[k] = (int) (sum / range);
        // update other valid averages using sliding window
        for (int i = k + 1; i < nums.length - k; ++i) {
            sum = sum - nums[i - k - 1] + nums[i + k];
            res[i] = (int) (sum / range);
        }
        return res;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).