2556. Disconnect Path in a Binary Matrix by at Most One Flip

Problem

You are given a 0-indexed m x n binary matrix grid. You can move from a cell (row, col) to any of the cells (row + 1, col) or (row, col + 1) that has the value 1. The matrix is disconnected if there is no path from (0, 0) to (m - 1, n - 1).

You can flip the value of at most one (possibly none) cell. You cannot flip the cells (0, 0) and (m - 1, n - 1).

Return true **if it is possible to make the matrix disconnect or *false* otherwise**.

Note that flipping a cell changes its value from 0 to 1 or from 1 to 0.

  Example 1:

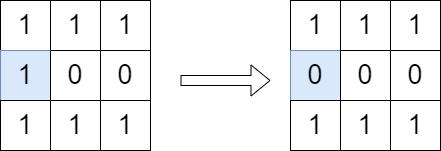
Input: grid = [[1,1,1],[1,0,0],[1,1,1]]
Output: true
Explanation: We can change the cell shown in the diagram above. There is no path from (0, 0) to (2, 2) in the resulting grid.

Example 2:

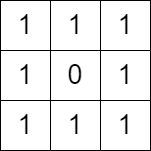
Input: grid = [[1,1,1],[1,0,1],[1,1,1]]
Output: false
Explanation: It is not possible to change at most one cell such that there is not path from (0, 0) to (2, 2).

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 1000

• 1 <= m * n <= 105

• grid[i][j] is either 0 or 1.

• grid[0][0] == grid[m - 1][n - 1] == 1

Solution (Java)

class Solution {
    public boolean isPossibleToCutPath(int[][] grid) {
        int first=dfs(grid,0,0);
        grid[0][0]=1; //reset for 2nd dfs() as got updated above
        int second=dfs(grid,0,0);
        return second >= 1 ? false : true;
    }

    private int dfs(int[][] g, int r, int c) {
        if(r == g.length-1 && c == g[0].length-1)
            return 1;
        if(r == g.length || c == g[0].length || g[r][c] == 0)
            return 0;

        g[r][c]=0;
        if(dfs(g,r+1,c) == 1)
            return 1;
        return dfs(g,r,c+1);
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).