Minimum Cost to Make at Least One Valid Path in a Grid

Problem

Given an m x n grid. Each cell of the grid has a sign pointing to the next cell you should visit if you are currently in this cell. The sign of grid[i][j] can be:

1 which means go to the cell to the right. (i.e go from grid[i][j] to grid[i][j + 1])
2 which means go to the cell to the left. (i.e go from grid[i][j] to grid[i][j - 1])
3 which means go to the lower cell. (i.e go from grid[i][j] to grid[i + 1][j])
4 which means go to the upper cell. (i.e go from grid[i][j] to grid[i - 1][j])

Notice that there could be some signs on the cells of the grid that point outside the grid.

You will initially start at the upper left cell (0, 0). A valid path in the grid is a path that starts from the upper left cell (0, 0) and ends at the bottom-right cell (m - 1, n - 1) following the signs on the grid. The valid path does not have to be the shortest.

You can modify the sign on a cell with cost = 1. You can modify the sign on a cell one time only.

Return the minimum cost to make the grid have at least one valid path.

Example 1:

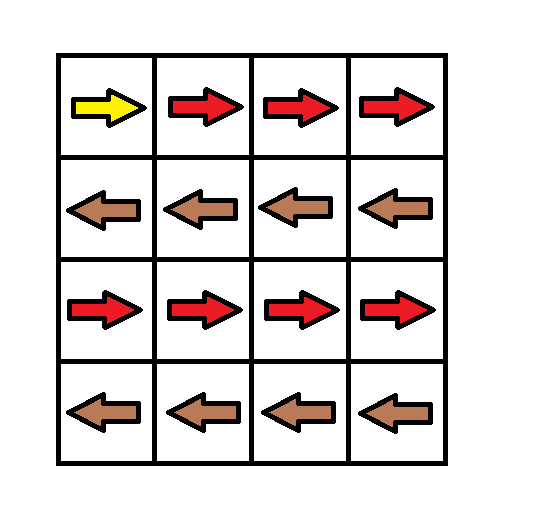
Input: grid = [[1,1,1,1],[2,2,2,2],[1,1,1,1],[2,2,2,2]]
Output: 3
Explanation: You will start at point (0, 0).
The path to (3, 3) is as follows. (0, 0) --> (0, 1) --> (0, 2) --> (0, 3) change the arrow to down with cost = 1 --> (1, 3) --> (1, 2) --> (1, 1) --> (1, 0) change the arrow to down with cost = 1 --> (2, 0) --> (2, 1) --> (2, 2) --> (2, 3) change the arrow to down with cost = 1 --> (3, 3)
The total cost = 3.

Example 2:

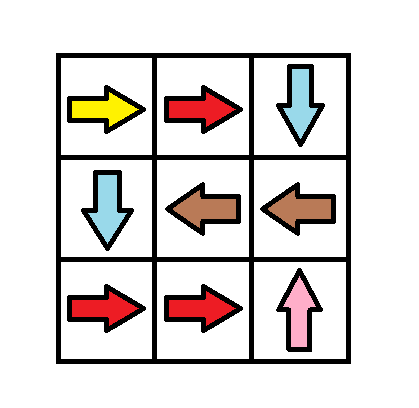
Input: grid = [[1,1,3],[3,2,2],[1,1,4]]
Output: 0
Explanation: You can follow the path from (0, 0) to (2, 2).

Example 3:

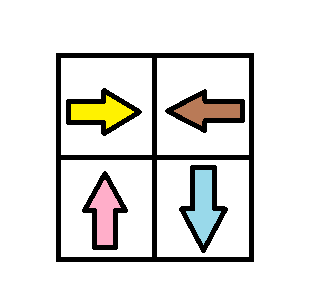
Input: grid = [[1,2],[4,3]]
Output: 1

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100
1 <= grid[i][j] <= 4

Solution

class Solution {
    private final int[][] dir = new int[][] {{0, 0}, {0, 1}, {0, -1}, {1, 0}, {-1, 0}};

    public int minCost(int[][] grid) {
        int[][] visited = new int[grid.length][grid[0].length];
        Queue<Pair> queue = new LinkedList<>();
        addAllTheNodeInRange(0, 0, grid, queue, visited);
        if (visited[grid.length - 1][grid[0].length - 1] == 1) {
            return 0;
        }
        int cost = 0;
        while (!queue.isEmpty()) {
            cost++;
            int size = queue.size();
            for (int i = 0; i < size; i++) {
                Pair pa = queue.poll();
                for (int k = 1; k < dir.length; k++) {
                    int m = Objects.requireNonNull(pa).x + dir[k][0];
                    int n = pa.y + dir[k][1];
                    addAllTheNodeInRange(m, n, grid, queue, visited);
                    if (visited[grid.length - 1][grid[0].length - 1] == 1) {
                        return cost;
                    }
                }
            }
        }
        return -1;
    }

    private void addAllTheNodeInRange(
            int x, int y, int[][] grid, Queue<Pair> queue, int[][] visited) {
        while (x >= 0
                && x < visited.length
                && y >= 0
                && y < visited[0].length
                && visited[x][y] == 0) {
            queue.offer(new Pair(x, y));
            visited[x][y]++;
            int[] d = dir[grid[x][y]];
            x += d[0];
            y += d[1];
        }
    }

    private static class Pair {
        int x;
        int y;

        public Pair(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).