2203. Minimum Weighted Subgraph With the Required Paths

Problem

You are given an integer n denoting the number of nodes of a weighted directed graph. The nodes are numbered from 0 to n - 1.

You are also given a 2D integer array edges where edges[i] = [fromi, toi, weighti] denotes that there exists a directed edge from fromi to toi with weight weighti.

Lastly, you are given three distinct integers src1, src2, and dest denoting three distinct nodes of the graph.

Return **the *minimum weight* of a subgraph of the graph such that it is possible to reach** dest from both src1 and src2 via a set of edges of this subgraph. In case such a subgraph does not exist, return -1.

A subgraph is a graph whose vertices and edges are subsets of the original graph. The weight of a subgraph is the sum of weights of its constituent edges.

  Example 1:

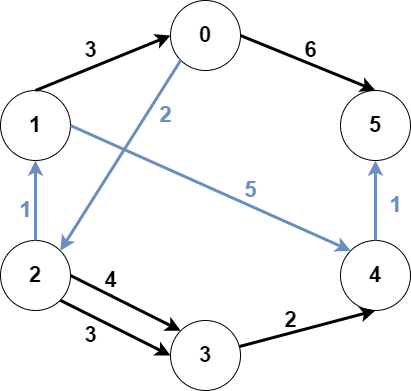
Input: n = 6, edges = [[0,2,2],[0,5,6],[1,0,3],[1,4,5],[2,1,1],[2,3,3],[2,3,4],[3,4,2],[4,5,1]], src1 = 0, src2 = 1, dest = 5
Output: 9
Explanation:
The above figure represents the input graph.
The blue edges represent one of the subgraphs that yield the optimal answer.
Note that the subgraph [[1,0,3],[0,5,6]] also yields the optimal answer. It is not possible to get a subgraph with less weight satisfying all the constraints.

Example 2:

Input: n = 3, edges = [[0,1,1],[2,1,1]], src1 = 0, src2 = 1, dest = 2
Output: -1
Explanation:
The above figure represents the input graph.
It can be seen that there does not exist any path from node 1 to node 2, hence there are no subgraphs satisfying all the constraints.

  Constraints:

• 3 <= n <= 10^5

• 0 <= edges.length <= 10^5

• edges[i].length == 3

• 0 <= fromi, toi, src1, src2, dest <= n - 1

• fromi != toi

• src1, src2, and dest are pairwise distinct.

• 1 <= weight[i] <= 10^5

Solution

class Solution {
    public long minimumWeight(int n, int[][] edges, int src1, int src2, int dest) {
        List<int[]>[] graph = new List[n];
        long[][] weight = new long[3][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < 3; j++) {
                weight[j][i] = Long.MAX_VALUE;
            }
            graph[i] = new ArrayList<>();
        }
        for (int[] e : edges) {
            graph[e[0]].add(new int[] {e[1], e[2]});
        }
        Queue<Node> queue = new PriorityQueue<>(Comparator.comparingLong(node -> node.weight));
        queue.offer(new Node(0, src1, 0));
        weight[0][src1] = 0;
        queue.offer(new Node(1, src2, 0));
        weight[1][src2] = 0;
        while (!queue.isEmpty()) {
            Node curr = queue.poll();
            if (curr.vertex == dest && curr.index == 2) {
                return curr.weight;
            }
            for (int[] next : graph[curr.vertex]) {
                if (curr.index == 2 && weight[curr.index][next[0]] > curr.weight + next[1]) {
                    weight[curr.index][next[0]] = curr.weight + next[1];
                    queue.offer(new Node(curr.index, next[0], weight[curr.index][next[0]]));
                } else if (weight[curr.index][next[0]] > curr.weight + next[1]) {
                    weight[curr.index][next[0]] = curr.weight + next[1];
                    queue.offer(new Node(curr.index, next[0], weight[curr.index][next[0]]));
                    if (weight[curr.index ^ 1][next[0]] != Long.MAX_VALUE
                            && weight[curr.index][next[0]] + weight[curr.index ^ 1][next[0]]
                                    < weight[2][next[0]]) {
                        weight[2][next[0]] =
                                weight[curr.index][next[0]] + weight[curr.index ^ 1][next[0]];
                        queue.offer(new Node(2, next[0], weight[2][next[0]]));
                    }
                }
            }
        }
        return -1;
    }

    private static class Node {
        int index;
        int vertex;
        long weight;

        Node(int index, int vertex, long weight) {
            this.index = index;
            this.vertex = vertex;
            this.weight = weight;
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).