Problem
There is a strange printer with the following two special requirements:
On each turn, the printer will print a solid rectangular pattern of a single color on the grid. This will cover up the existing colors in the rectangle.
Once the printer has used a color for the above operation, the same color cannot be used again.
You are given a m x n matrix targetGrid, where targetGrid[row][col] is the color in the position (row, col) of the grid.
Return true** if it is possible to print the matrix targetGrid,**** otherwise, return **false.
Example 1:
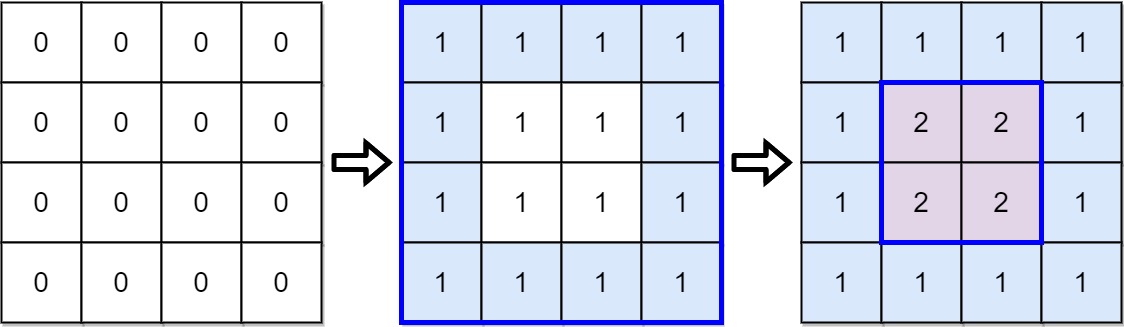
Input: targetGrid = [[1,1,1,1],[1,2,2,1],[1,2,2,1],[1,1,1,1]]
Output: true
Example 2:
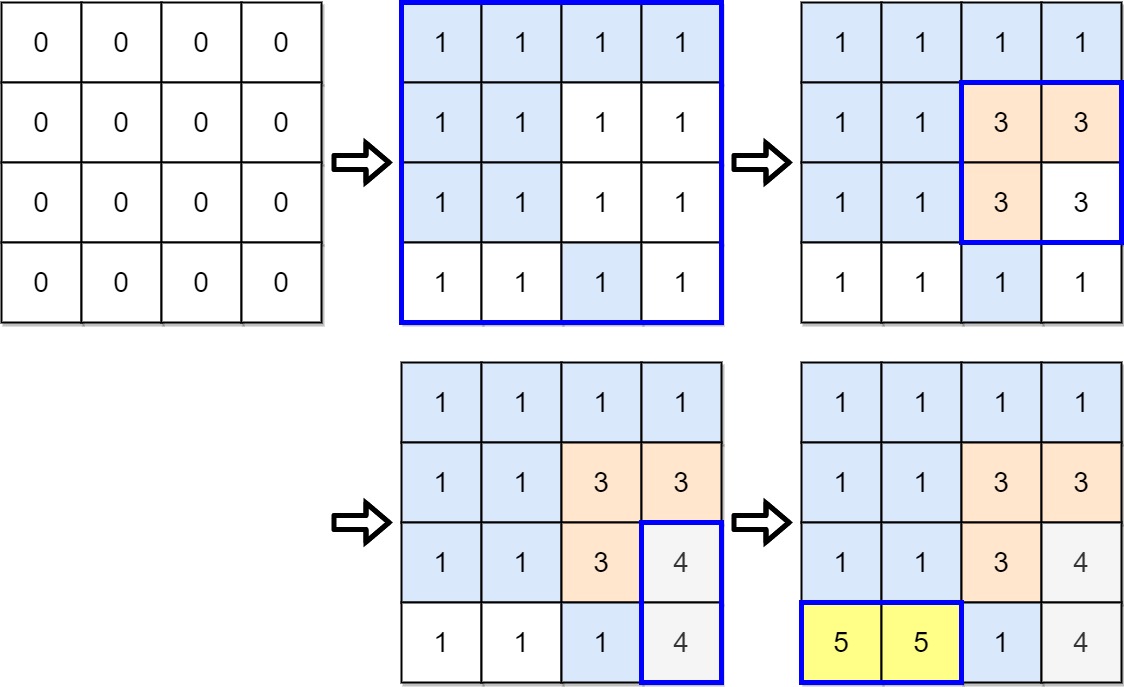
Input: targetGrid = [[1,1,1,1],[1,1,3,3],[1,1,3,4],[5,5,1,4]]
Output: true
Example 3:
Input: targetGrid = [[1,2,1],[2,1,2],[1,2,1]]
Output: false
Explanation: It is impossible to form targetGrid because it is not allowed to print the same color in different turns.
Constraints:
m == targetGrid.lengthn == targetGrid[i].length1 <= m, n <= 601 <= targetGrid[row][col] <= 60
Solution
class Solution {
public boolean isPrintable(int[][] targetGrid) {
int[][] colorBound = new int[61][4];
Set<Integer> colors = new HashSet<>();
// prepare colorBound with Max and Min integer for later compare
for (int i = 0; i < colorBound.length; i++) {
for (int j = 0; j < colorBound[0].length; j++) {
if (j == 0 || j == 1) {
colorBound[i][j] = Integer.MAX_VALUE;
} else {
colorBound[i][j] = Integer.MIN_VALUE;
}
}
}
// find the color range for each color
// each color i has a colorBound[i] with {min_i, min_j, max_i, max_j}
for (int i = 0; i < targetGrid.length; i++) {
for (int j = 0; j < targetGrid[0].length; j++) {
colorBound[targetGrid[i][j]][0] = Math.min(colorBound[targetGrid[i][j]][0], i);
colorBound[targetGrid[i][j]][1] = Math.min(colorBound[targetGrid[i][j]][1], j);
colorBound[targetGrid[i][j]][2] = Math.max(colorBound[targetGrid[i][j]][2], i);
colorBound[targetGrid[i][j]][3] = Math.max(colorBound[targetGrid[i][j]][3], j);
colors.add(targetGrid[i][j]);
}
}
boolean[] printed = new boolean[61];
boolean[][] visited = new boolean[targetGrid.length][targetGrid[0].length];
// DFS all the colors, skip the color already be printed
for (Integer color : colors) {
if (printed[color]) {
continue;
}
if (!dfs(targetGrid, printed, colorBound, visited, color)) {
return false;
}
}
// if all color has been printed, then return true
return true;
}
private boolean dfs(
int[][] targetGrid,
boolean[] printed,
int[][] colorBound,
boolean[][] visited,
int color) {
printed[color] = true;
for (int i = colorBound[color][0]; i <= colorBound[color][2]; i++) {
for (int j = colorBound[color][1]; j <= colorBound[color][3]; j++) {
// if i, j is already visited, skip
if (visited[i][j]) {
continue;
}
// if we find a different color, then check if the color is already printed, if so,
// return false
// otherwise, dfs the range of the new color
if (targetGrid[i][j] != color) {
if (printed[targetGrid[i][j]]) {
return false;
}
if (!dfs(targetGrid, printed, colorBound, visited, targetGrid[i][j])) {
return false;
}
}
visited[i][j] = true;
}
}
return true;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).