2397. Maximum Rows Covered by Columns

Problem

You are given a 0-indexed m x n binary matrix matrix and an integer numSelect, which denotes the number of distinct columns you must select from matrix.

Let us consider s = {c1, c2, ...., cnumSelect} as the set of columns selected by you. A row row is covered by s if:

• For each cell matrix[row][col] (0 <= col <= n - 1) where matrix[row][col] == 1, col is present in s or,

• No cell in row has a value of 1.

You need to choose numSelect columns such that the number of rows that are covered is maximized.

Return **the *maximum* number of rows that can be covered by a set of numSelect columns.**

  Example 1:

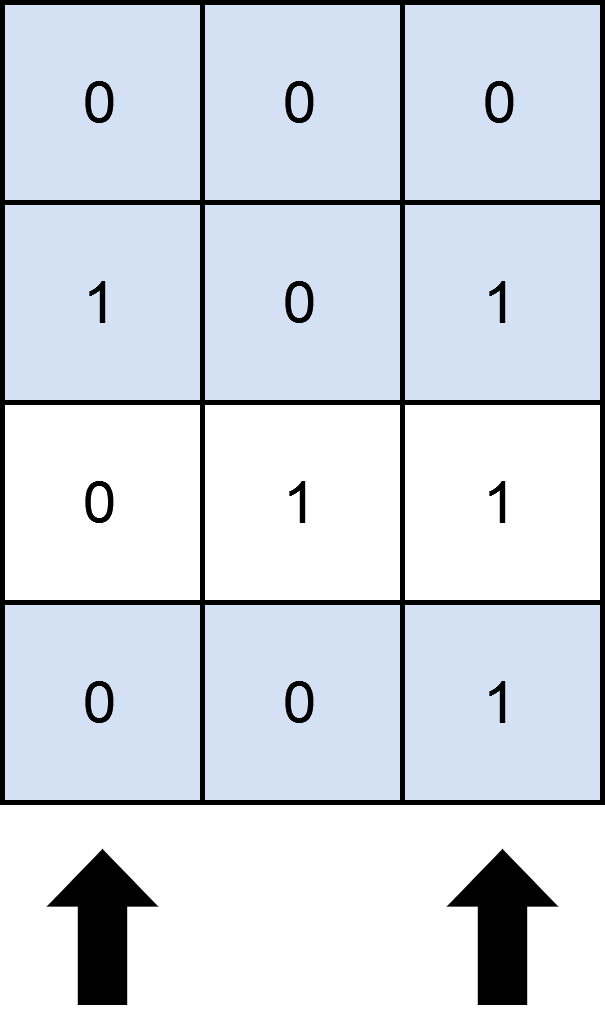
Input: matrix = [[0,0,0],[1,0,1],[0,1,1],[0,0,1]], numSelect = 2
Output: 3
Explanation: One possible way to cover 3 rows is shown in the diagram above.
We choose s = {0, 2}.
- Row 0 is covered because it has no occurrences of 1.
- Row 1 is covered because the columns with value 1, i.e. 0 and 2 are present in s.
- Row 2 is not covered because matrix[2][1] == 1 but 1 is not present in s.
- Row 3 is covered because matrix[2][2] == 1 and 2 is present in s.
Thus, we can cover three rows.
Note that s = {1, 2} will also cover 3 rows, but it can be shown that no more than three rows can be covered.

Example 2:

Input: matrix = [[1],[0]], numSelect = 1
Output: 2
Explanation: Selecting the only column will result in both rows being covered since the entire matrix is selected.
Therefore, we return 2.

  Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= m, n <= 12

• matrix[i][j] is either 0 or 1.

• 1 <= numSelect&nbsp;<= n

Solution (Java)

class Solution {
    public int maximumRows(int[][] mat, int cols) {

        int m=mat.length;
        int n=mat[0].length;

        int[] s=new int[n];

        return f(0,m,n,cols,mat,s);
    }

    public int f(int ind,int m,int n,int cols,int[][] mat,int[] s){

        if(cols==0){
            int count=0;
            for(int i=0; i<m; i++){
            //supposing that this row is valid
                boolean selected=true;
                for(int j=0; j<n; j++){
                //if any cell of this row violates the given two conditions, then the row is discarded
                    if(mat[i][j]==1 && s[j]!=1)
                        selected=false;
                }
                if(selected)
                    count+=1;
            }

            return count;
        }

        int ans=-1;
        for(int i=ind; i<n; i++){

            s[i]=1; //do
            ans=Math.max(ans,f(i+1,m,n,cols-1,mat,s));
            s[i]=0; //undo / backtrack
        }

        return ans;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).