363. Max Sum of Rectangle No Larger Than K

Problem

Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.

It is guaranteed that there will be a rectangle with a sum no larger than k.

  Example 1:

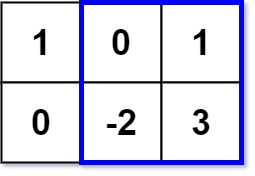
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).

Example 2:

Input: matrix = [[2,2,-1]], k = 3
Output: 3

  Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= m, n <= 100

• -100 <= matrix[i][j] <= 100

• -10^5 <= k <= 10^5

  Follow up: What if the number of rows is much larger than the number of columns?

Solution

class Solution {
    public int maxSumSubmatrix(int[][] matrix, int k) {
        int m = matrix.length, n = matrix[0].length;
        int res = Integer.MIN_VALUE;
        for (int c1 = 0; c1 < n; c1++) {
            int[] presum = new int[m];
            for (int c2 = c1; c2 < n; c2++) {
                TreeSet<Integer> set = new TreeSet<Integer>();
                set.add(0);
                int val = 0;
                for (int r = 0; r < m; r++) {
                    presum[r] += matrix[r][c2];
                    val += presum[r];
                    Integer prev = set.ceiling(val - k);
                    if (prev != null) {
                        res = Math.max(res, val - prev);
                    }
                    set.add(val);
                }
            }
        }
        return res;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).