Problem
You are given an m x n binary matrix grid. An island is a group of 1's (representing land) connected 4-directionally (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
The area of an island is the number of cells with a value 1 in the island.
Return **the maximum *area* of an island in **grid. If there is no island, return 0.
Example 1:
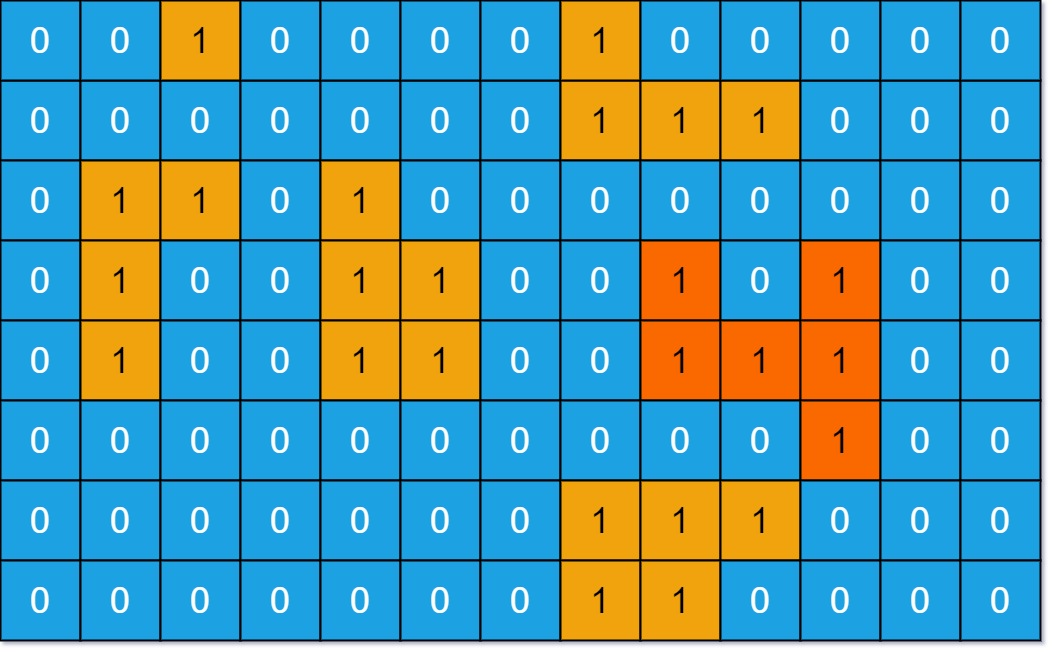
Input: grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
Output: 6
Explanation: The answer is not 11, because the island must be connected 4-directionally.
Example 2:
Input: grid = [[0,0,0,0,0,0,0,0]]
Output: 0
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 50grid[i][j]is either0or1.
Solution (Java)
class Solution {
public int maxAreaOfIsland(int[][] grid) {
if (grid == null || grid.length == 0) {
return 0;
}
int m = grid.length;
int n = grid[0].length;
int max = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (grid[i][j] == 1) {
int area = dfs(grid, i, j, m, n, 0);
max = Math.max(area, max);
}
}
}
return max;
}
private int dfs(int[][] grid, int i, int j, int m, int n, int area) {
if (i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == 0) {
return area;
}
grid[i][j] = 0;
area++;
area = dfs(grid, i + 1, j, m, n, area);
area = dfs(grid, i, j + 1, m, n, area);
area = dfs(grid, i - 1, j, m, n, area);
area = dfs(grid, i, j - 1, m, n, area);
return area;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).