1727. Largest Submatrix With Rearrangements

Problem

You are given a binary matrix matrix of size m x n, and you are allowed to rearrange the columns of the matrix in any order.

Return **the area of the largest submatrix within *matrix* where every element of the submatrix is 1 after reordering the columns optimally.**

  Example 1:

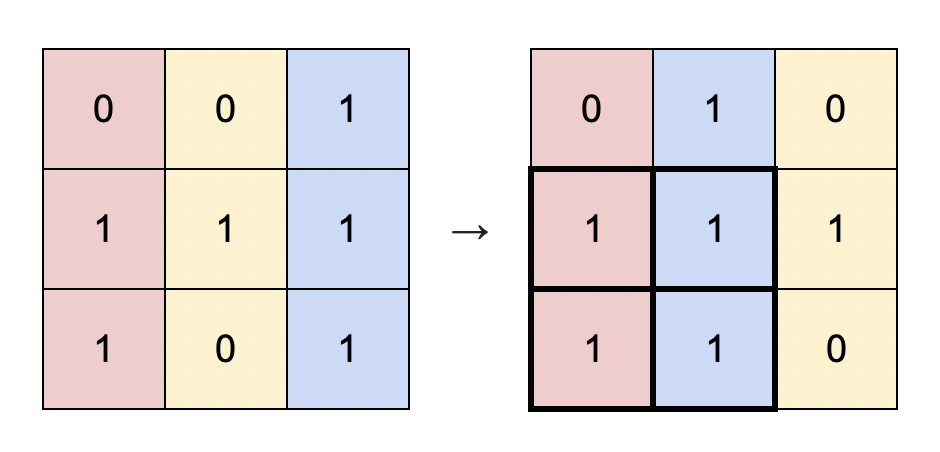
Input: matrix = [[0,0,1],[1,1,1],[1,0,1]]
Output: 4
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 4.

Example 2:

Input: matrix = [[1,0,1,0,1]]
Output: 3
Explanation: You can rearrange the columns as shown above.
The largest submatrix of 1s, in bold, has an area of 3.

Example 3:

Input: matrix = [[1,1,0],[1,0,1]]
Output: 2
Explanation: Notice that you must rearrange entire columns, and there is no way to make a submatrix of 1s larger than an area of 2.

  Constraints:

• m == matrix.length

• n == matrix[i].length

• 1 <= m * n <= 10^5

• matrix[i][j] is either 0 or 1.

Solution (Java)

class Solution {
    public int largestSubmatrix(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] != 0) {
                    matrix[i][j] = matrix[i - 1][j] + 1;
                }
            }
        }
        int count = 0;
        for (int[] ints : matrix) {
            Arrays.sort(ints);
            for (int j = 1; j <= n; j++) {
                count = Math.max(count, j * ints[n - j]);
            }
        }
        return count;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).