Largest Color Value in a Directed Graph

Problem

There is a directed graph of n colored nodes and m edges. The nodes are numbered from 0 to n - 1.

You are given a string colors where colors[i] is a lowercase English letter representing the color of the ith node in this graph (0-indexed). You are also given a 2D array edges where edges[j] = [aj, bj] indicates that there is a directed edge from node aj to node bj.

A valid path in the graph is a sequence of nodes x1 -> x2 -> x3 -> ... -> xk such that there is a directed edge from xi to xi+1 for every 1 <= i < k. The color value of the path is the number of nodes that are colored the most frequently occurring color along that path.

Return **the *largest color value* of any valid path in the given graph, or -1 if the graph contains a cycle**.

Example 1:

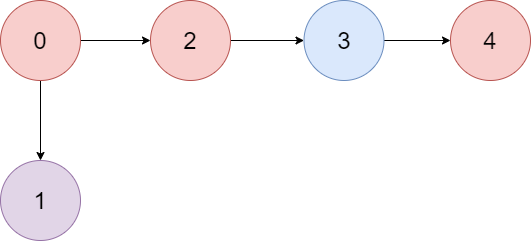
Input: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
Output: 3
Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored "a" (red in the above image).

Example 2:

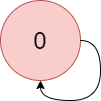
Input: colors = "a", edges = [[0,0]]
Output: -1
Explanation: There is a cycle from 0 to 0.

Constraints:

n == colors.length
m == edges.length
1 <= n <= 10^5
0 <= m <= 10^5
colors consists of lowercase English letters.
0 <= aj, bj < n

Solution

class Solution {
    public int largestPathValue(String colors, int[][] edges) {
        int len = colors.length();
        List<Integer>[] graph = buildGraph(len, edges);
        int[] frequencies = new int[26];
        HashMap<Integer, int[]> calculatedFrequencies = new HashMap<>();
        int[] status = new int[len];
        for (int i = 0; i < len; i++) {
            if (status[i] != 0) {
                continue;
            }
            int[] localMax = runDFS(graph, i, calculatedFrequencies, status, colors);
            if (localMax[26] == -1) {
                Arrays.fill(frequencies, -1);
                break;
            } else {
                for (int color = 0; color < 26; color++) {
                    frequencies[color] = Math.max(frequencies[color], localMax[color]);
                }
            }
        }
        int max = Integer.MIN_VALUE;
        for (int freq : frequencies) {
            max = Math.max(max, freq);
        }
        return max;
    }

    private int[] runDFS(
            List<Integer>[] graph,
            int node,
            HashMap<Integer, int[]> calculatedFrequencies,
            int[] status,
            String colors) {
        if (calculatedFrequencies.containsKey(node)) {
            return calculatedFrequencies.get(node);
        }
        int[] frequencies = new int[27];
        if (status[node] == 1) {
            frequencies[26] = -1;
            return frequencies;
        }
        status[node] = 1;
        for (int neighbour : graph[node]) {
            int[] localMax = runDFS(graph, neighbour, calculatedFrequencies, status, colors);
            if (localMax[26] == -1) {
                return localMax;
            }
            for (int i = 0; i < 26; i++) {
                frequencies[i] = Math.max(frequencies[i], localMax[i]);
            }
        }
        status[node] = 2;
        int color = colors.charAt(node) - 'a';
        frequencies[color]++;
        calculatedFrequencies.put(node, frequencies);
        return frequencies;
    }

    private List<Integer>[] buildGraph(int n, int[][] edges) {
        List<Integer>[] graph = new ArrayList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
        for (int[] edge : edges) {
            graph[edge[0]].add(edge[1]);
        }
        return graph;
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).