Problem
You are given a 0-indexed 2D matrix grid of size n x n, where (r, c) represents:
- A cell containing a thief if
grid[r][c] = 1 - An empty cell if
grid[r][c] = 0
You are initially positioned at cell (0, 0). In one move, you can move to any adjacent cell in the grid, including cells containing thieves.
The safeness factor of a path on the grid is defined as the minimum manhattan distance from any cell in the path to any thief in the grid.
Return **the *maximum safeness factor* of all paths leading to cell (n - 1, n - 1).**
An adjacent cell of cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) and (r - 1, c) if it exists.
The Manhattan distance between two cells (a, b) and (x, y) is equal to |a - x| + |b - y|, where |val| denotes the absolute value of val.
Example 1:
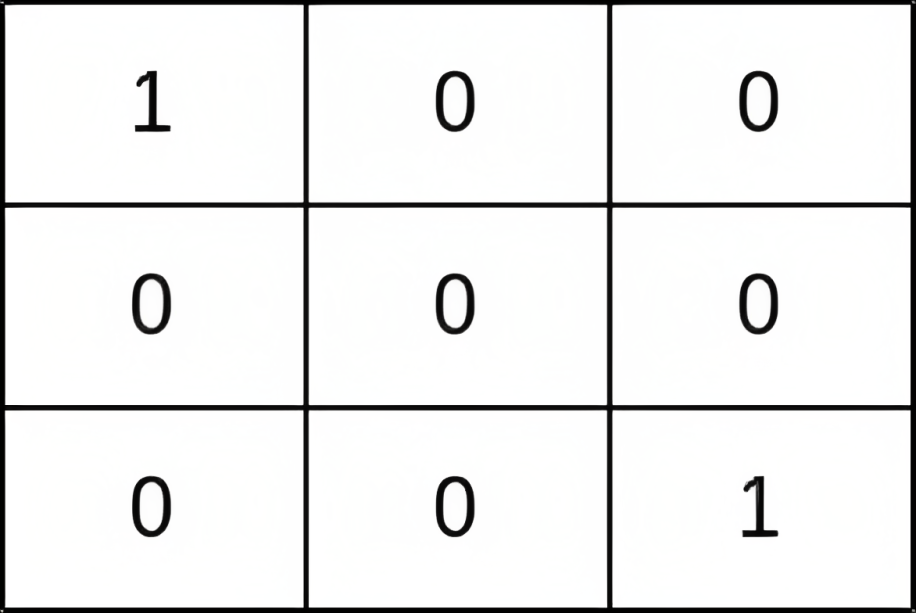
Input: grid = [[1,0,0],[0,0,0],[0,0,1]]
Output: 0
Explanation: All paths from (0, 0) to (n - 1, n - 1) go through the thieves in cells (0, 0) and (n - 1, n - 1).
Example 2:
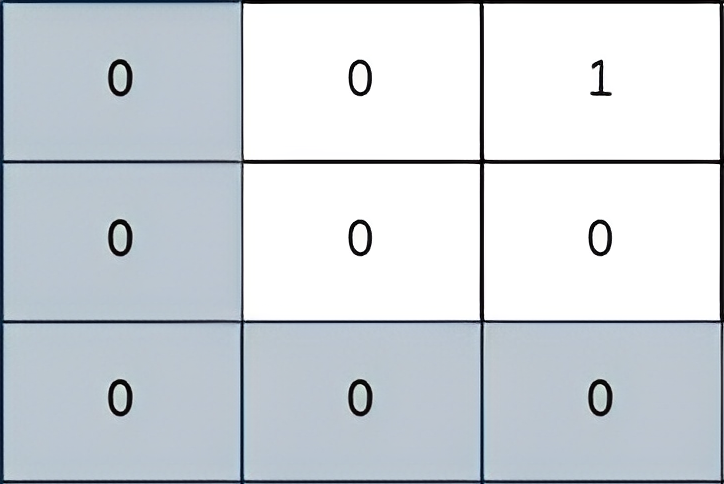
Input: grid = [[0,0,1],[0,0,0],[0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 2) is cell (0, 0). The distance between them is | 0 - 0 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.
Example 3:
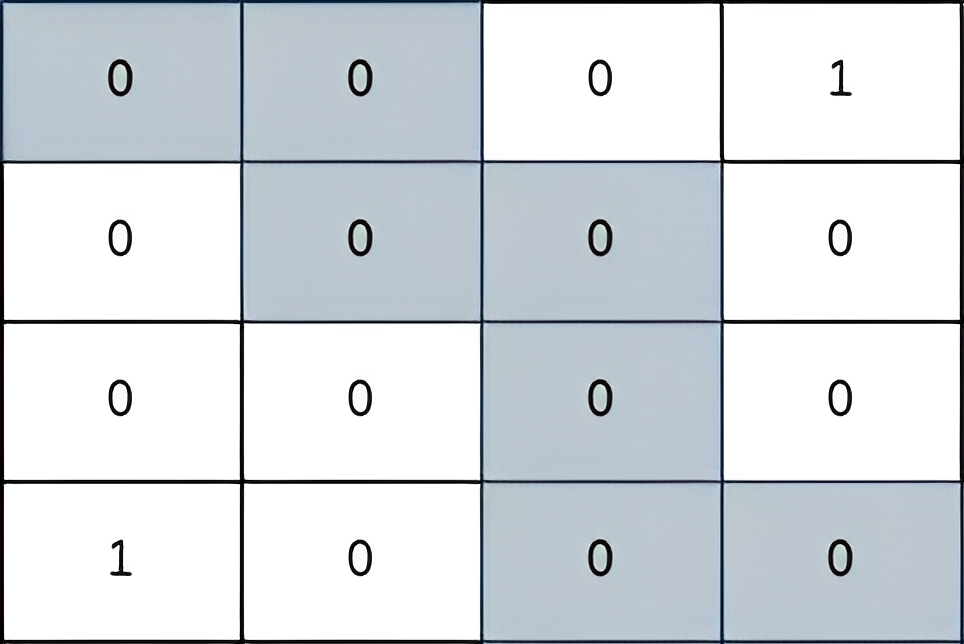
Input: grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 3) is cell (1, 2). The distance between them is | 0 - 1 | + | 3 - 2 | = 2.
- The closest cell of the path to the thief at cell (3, 0) is cell (3, 2). The distance between them is | 3 - 3 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.
Constraints:
1 <= grid.length == n <= 400grid[i].length == ngrid[i][j]is either0or1.- There is at least one thief in the
grid.
Solution (Java)
class Solution {
// directions
int[][] dirArr = new int[][]{{0,1}, {0,-1}, {1,0}, {-1,0}};
public int maximumSafenessFactor(List<List<Integer>> grid) {
int m = grid.size();
int n = grid.get(0).size();
int[][] mat = new int[m][n];
for(int i=0;i<m;i++)
for(int j=0;j<n;j++)
mat[i][j]=grid.get(i).get(j);
// no path possible
if(mat[0][0]==1 || mat[m-1][n-1]==1)return 0;
// pre-populate safety
int[][] safety = new int[m][n];
Queue<int[]> queue = new LinkedList<>();
for(int i=0;i<m;i++)
for(int j=0;j<n;j++){
if(mat[i][j]==1){
queue.add(new int[]{i,j,0});
// since node has thief himself
safety[i][j]=0;
} else safety[i][j]=Integer.MAX_VALUE;
}
// bfs to fill safety for all nodes
while(!queue.isEmpty()){
int size = queue.size();
while(size-->0){
int[] curr = queue.poll();
int currx = curr[0];
int curry = curr[1];
for(int[] dir:dirArr){
int nextx = currx+dir[0];
int nexty = curry+dir[1];
if(isValid(nextx, nexty, mat) && curr[2]+1 < safety[nextx][nexty]){
queue.add(new int[]{nextx, nexty, curr[2]+1});
safety[nextx][nexty]=curr[2]+1;
}
}
}
}
// bfs to find safest path
Queue<int[]> path = new PriorityQueue<>(new Comparator<>(){
@Override
public int compare(int[] a, int[] b){
return b[2]-a[2];
}
});
path.add(new int[]{0, 0, safety[0][0]});
mat[0][0]=2;
int minSafety = 0;
while(!path.isEmpty()){
int size = path.size();
while(size-->0){
int[] curr = path.poll();
int currx = curr[0];
int curry = curr[1];
int currSafety = curr[2];
if(currx==m-1 && curry==n-1)return currSafety;
for(int[] dir:dirArr){
int nextx = currx+dir[0];
int nexty = curry+dir[1];
if(isValid(nextx, nexty, mat) && mat[nextx][nexty]!=2){
path.add(new int[]{nextx, nexty, Math.min(currSafety, safety[nextx][nexty])});
mat[nextx][nexty]=2;
}
}
}
}
return minSafety;
}
private boolean isValid(int i, int j, int[][] mat){
return i>=0 && i<mat.length && j>=0 && j<mat[i].length;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).