Problem
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
A route's effort is the maximum absolute difference** **in heights between two consecutive cells of the route.
Return **the minimum *effort* required to travel from the top-left cell to the bottom-right cell.**
Example 1:
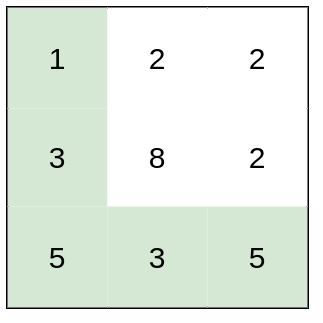
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
Example 2:
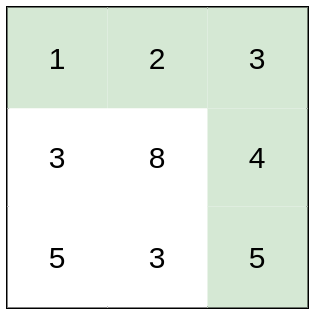
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
Example 3:
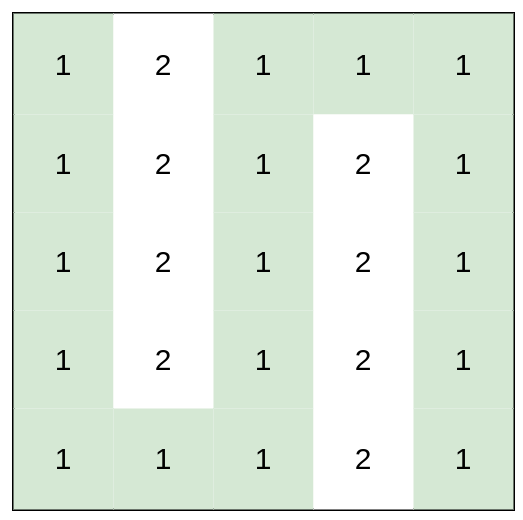
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.
Constraints:
rows == heights.lengthcolumns == heights[i].length1 <= rows, columns <= 1001 <= heights[i][j] <= 10^6
Solution (Java)
class Solution {
private static class Pair implements Comparable<Pair> {
int row;
int col;
int diff;
Pair(int row, int col, int diff) {
this.row = row;
this.col = col;
this.diff = diff;
}
public int compareTo(Pair o) {
return this.diff - o.diff;
}
}
public int minimumEffortPath(int[][] heights) {
int n = heights.length;
int m = heights[0].length;
PriorityQueue<Pair> pq = new PriorityQueue<>();
pq.add(new Pair(0, 0, 0));
boolean[][] vis = new boolean[n][m];
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
int min = Integer.MAX_VALUE;
while (!pq.isEmpty()) {
Pair p = pq.remove();
int row = p.row;
int col = p.col;
int diff = p.diff;
if (vis[row][col]) {
continue;
}
vis[row][col] = true;
if (row == n - 1 && col == m - 1) {
min = Math.min(min, diff);
}
for (int i = 0; i < 4; i++) {
int r = row + dx[i];
int c = col + dy[i];
if (r < 0 || c < 0 || r >= n || c >= m || vis[r][c]) {
continue;
}
pq.add(new Pair(r, c, Math.max(diff, Math.abs(heights[r][c] - heights[row][col]))));
}
}
return min;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).