913. Cat and Mouse

Problem

A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.

The graph is given as follows: graph[a] is a list of all nodes b such that ab is an edge of the graph.

The mouse starts at node 1 and goes first, the cat starts at node 2 and goes second, and there is a hole at node 0.

During each player's turn, they must travel along one edge of the graph that meets where they are.  For example, if the Mouse is at node 1, it must travel to any node in graph[1].

Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)

Then, the game can end in three ways:

• If ever the Cat occupies the same node as the Mouse, the Cat wins.

• If ever the Mouse reaches the Hole, the Mouse wins.

• If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player's turn to move), the game is a draw.

Given a graph, and assuming both players play optimally, return

• 1 if the mouse wins the game,

• 2 if the cat wins the game, or

• 0 if the game is a draw.

  Example 1:

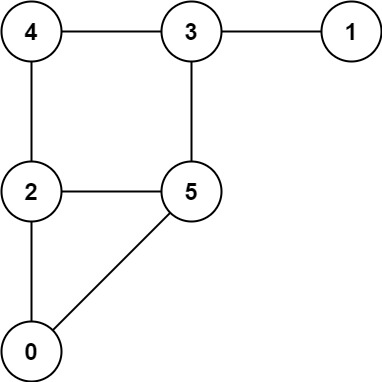
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
Output: 0

Example 2:

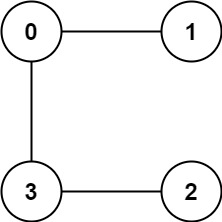
Input: graph = [[1,3],[0],[3],[0,2]]
Output: 1

  Constraints:

• 3 <= graph.length <= 50

• 1&nbsp;<= graph[i].length < graph.length

• 0 <= graph[i][j] < graph.length

• graph[i][j] != i

• graph[i] is unique.

• The mouse and the cat can always move. 

Solution

class Solution {
    private static final int DRAW = 0;
    private static final int MOUSE_WIN = 1;
    private static final int CAT_WIN = 2;
    private static final int MOUSE = 0;
    private static final int CAT = 1;

    public int catMouseGame(int[][] graph) {
        int n = graph.length;
        int[][][] states = new int[n][n][2];
        int[][][] degree = new int[n][n][2];
        for (int m = 0; m < n; ++m) {
            for (int c = 0; c < n; ++c) {
                degree[m][c][MOUSE] = graph[m].length;
                degree[m][c][CAT] = graph[c].length;
                for (int node : graph[c]) {
                    if (node == 0) {
                        --degree[m][c][CAT];
                        break;
                    }
                }
            }
        }
        Queue<int[]> q = new LinkedList<>();
        for (int i = 1; i < n; ++i) {
            states[0][i][MOUSE] = MOUSE_WIN;
            states[0][i][CAT] = MOUSE_WIN;
            states[i][i][MOUSE] = CAT_WIN;
            states[i][i][CAT] = CAT_WIN;
            q.offer(new int[] {0, i, MOUSE, MOUSE_WIN});
            q.offer(new int[] {i, i, MOUSE, CAT_WIN});
            q.offer(new int[] {0, i, CAT, MOUSE_WIN});
            q.offer(new int[] {i, i, CAT, CAT_WIN});
        }
        while (!q.isEmpty()) {
            int[] state = q.poll();
            int mouse = state[0];
            int cat = state[1];
            int turn = state[2];
            int result = state[3];
            if (mouse == 1 && cat == 2 && turn == MOUSE) {
                return result;
            }
            int prevTurn = 1 - turn;
            for (int prev : graph[prevTurn == MOUSE ? mouse : cat]) {
                int prevMouse = prevTurn == MOUSE ? prev : mouse;
                int prevCat = prevTurn == CAT ? prev : cat;
                if (prevCat != 0
                        && states[prevMouse][prevCat][prevTurn] == DRAW
                        && (prevTurn == MOUSE && result == MOUSE_WIN
                                || prevTurn == CAT && result == CAT_WIN
                                || --degree[prevMouse][prevCat][prevTurn] == 0)) {
                    states[prevMouse][prevCat][prevTurn] = result;
                    q.offer(new int[] {prevMouse, prevCat, prevTurn, result});
                }
            }
        }
        return DRAW;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).