2392. Build a Matrix With Conditions

Problem

You are given a positive integer k. You are also given:

• a 2D integer array rowConditions of size n where rowConditions[i] = [abovei, belowi], and

• a 2D integer array colConditions of size m where colConditions[i] = [lefti, righti].

The two arrays contain integers from 1 to k.

You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.

The matrix should also satisfy the following conditions:

• The number abovei should appear in a row that is strictly above the row at which the number belowi appears for all i from 0 to n - 1.

• The number lefti should appear in a column that is strictly left of the column at which the number righti appears for all i from 0 to m - 1.

Return *any matrix that satisfies the conditions*. If no answer exists, return an empty matrix.

  Example 1:

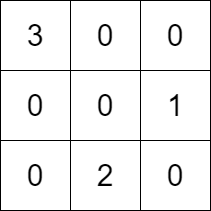
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]
Output: [[3,0,0],[0,0,1],[0,2,0]]
Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions.
The row conditions are the following:
- Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.
- Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.
The column conditions are the following:
- Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.
- Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.
Note that there may be multiple correct answers.

Example 2:

Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]
Output: []
Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.
No matrix can satisfy all the conditions, so we return the empty matrix.

  Constraints:

• 2 <= k <= 400

• 1 <= rowConditions.length, colConditions.length <= 10^4

• rowConditions[i].length == colConditions[i].length == 2

• 1 <= abovei, belowi, lefti, righti <= k

• abovei != belowi

• lefti != righti

Solution

class Solution {
    List<Integer>[] al;

    public int[][] buildMatrix(int k, int[][] rc, int[][] cc) {

        int ans[][] = new int[k][k];
        this.al = new ArrayList[k+1];

        for(int i=0;i<=k;i++) al[i] = new ArrayList<>();
        for(int r[] : rc) al[r[0]].add(r[1]);

        boolean[] vis = new boolean[k+1];
        boolean dfsvis[] = new boolean[k+1];
        List<Integer> rowStack = new ArrayList<>();

        for(int node=1;node<=k;node++){
            if(!vis[node]) {
                if(!dfs(node,vis,rowStack,dfsvis)) return new int[0][0];
            }
        }

        for(int i=0;i<=k;i++) al[i] = new ArrayList<>();
        for(int c[] : cc) al[c[0]].add(c[1]);
        List<Integer> colStack = new ArrayList<>();

        vis = new boolean[k+1];
        dfsvis = new boolean[k+1];

        for(int node=1;node<=k;node++){
            if(!vis[node]) {
                if(!dfs(node,vis,colStack,dfsvis)) return new int[0][0];
            }
        }

        HashMap<Integer,Integer> map = new HashMap<>();

        for(int i=0;i<colStack.size();i++){
            map.put(colStack.get(i),i);
        }

        int row = 0;

        for(int i=rowStack.size()-1;i>=0;i--){
            // should place this value leaving required cells ahead for other values to come to make column condition true. 
            ans[row++][k-map.get(rowStack.get(i))-1] = rowStack.get(i);
        }

        return ans;

    }

    // toposort dfs along with cycle check (returns false if cycle exists)
    private boolean dfs(int node,boolean[] vis,List<Integer> stack,boolean[] dfsvis){
        vis[node] = true;
        dfsvis[node] = true;
        for(int next : al[node]){
            if(!vis[next]) {
                if(!dfs(next,vis,stack,dfsvis)) return false;
            }else if(dfsvis[next]) return false;
        }
        stack.add(node);
        dfsvis[node] = false;
        return true;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).