782. Transform to Chessboard

Problem

You are given an n x n binary grid board. In each move, you can swap any two rows with each other, or any two columns with each other.

Return **the minimum number of moves to transform the board into a *chessboard board***. If the task is impossible, return -1.

A chessboard board is a board where no 0's and no 1's are 4-directionally adjacent.

  Example 1:

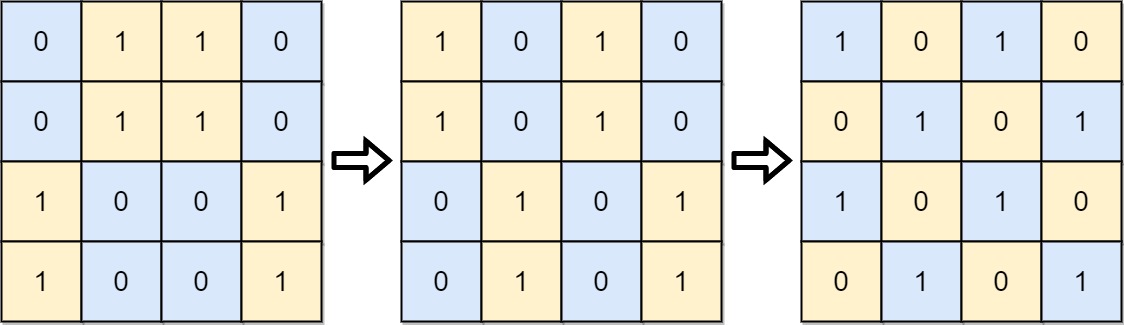
Input: board = [[0,1,1,0],[0,1,1,0],[1,0,0,1],[1,0,0,1]]
Output: 2
Explanation: One potential sequence of moves is shown.
The first move swaps the first and second column.
The second move swaps the second and third row.

Example 2:

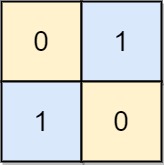
Input: board = [[0,1],[1,0]]
Output: 0
Explanation: Also note that the board with 0 in the top left corner, is also a valid chessboard.

Example 3:

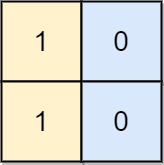
Input: board = [[1,0],[1,0]]
Output: -1
Explanation: No matter what sequence of moves you make, you cannot end with a valid chessboard.

  Constraints:

• n == board.length

• n == board[i].length

• 2 <= n <= 30

• board[i][j] is either 0 or 1.

Solution (Java)

class Solution {
    public int movesToChessboard(int[][] board) {
        int n = board.length;
        int colToMove = 0;
        int rowToMove = 0;
        int rowOneCnt = 0;
        int colOneCnt = 0;
        for (int[] ints : board) {
            for (int j = 0; j < n; j++) {
                if (((board[0][0] ^ ints[0]) ^ (ints[j] ^ board[0][j])) == 1) {
                    return -1;
                }
            }
        }
        for (int i = 0; i < n; i++) {
            rowOneCnt += board[0][i];
            colOneCnt += board[i][0];
            if (board[i][0] == i % 2) {
                rowToMove++;
            }
            if (board[0][i] == i % 2) {
                colToMove++;
            }
        }
        if (rowOneCnt < n / 2 || rowOneCnt > (n + 1) / 2) {
            return -1;
        }
        if (colOneCnt < n / 2 || colOneCnt > (n + 1) / 2) {
            return -1;
        }
        if (n % 2 == 1) {
            // we cannot make it when ..ToMove is odd
            if (colToMove % 2 == 1) {
                colToMove = n - colToMove;
            }
            if (rowToMove % 2 == 1) {
                rowToMove = n - rowToMove;
            }
        } else {
            colToMove = Math.min(colToMove, n - colToMove);
            rowToMove = Math.min(rowToMove, n - rowToMove);
        }
        return (colToMove + rowToMove) / 2;
    }
}

Solution (C++)

class Solution {
public:
   int movesToChessboard(vector<vector<int>>& b) {
      int n = b.size();
      for(int i = 0; i < n; i++){
         for(int j = 0; j < n; j++){
            if(b[0][0] ^ b[0][j] ^ b[i][0] ^ b[i][j]) return -1;
         }
      }
      int rowSum = 0;
      int colSum = 0;
      int rowSwap = 0;
      int colSwap = 0;
      for(int i = 0; i < n; i++){
         rowSum += b[i][0];
         colSum += b[0][i];
         rowSwap += b[i][0] == i % 2;
         colSwap += b[0][i] == i % 2;
      }
      if(rowSum != n/2 && rowSum != (n + 1)/2)return -1;
      if(colSum != n/2 && colSum != (n + 1)/2)return -1;
      if(n % 2 == 1){
         if(colSwap % 2) colSwap = n - colSwap;
         if(rowSwap % 2) rowSwap = n - rowSwap;
      }else{
         colSwap = min(colSwap, n - colSwap);
         rowSwap = min(rowSwap, n - rowSwap);
      }
      return (rowSwap + colSwap)/2;
   }
};

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).