1329. Sort the Matrix Diagonally

Problem

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

  Example 1:

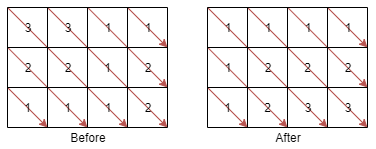
Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

  Constraints:

• m == mat.length

• n == mat[i].length

• 1 <= m, n <= 100

• 1 <= mat[i][j] <= 100

Solution

/**
 * @param {number[][]} mat
 * @return {number[][]}
 */
var diagonalSort = function(mat) {
    let y = mat.length, x = mat[0].length - 1,
        diag = new Uint8Array(y), k
    for (let i = 2 - y; i < x; i++) {
        diag.fill(101), k = 0
        for (let j = 0; j < y; j++)
            if (i+j >= 0 && i+j <= x)
                diag[k++] = mat[j][i+j]
        diag.sort(), k = 0
        for (let j = 0; j < y; j++)
            if (i+j >= 0 && i+j <= x)
                mat[j][i+j] = diag[k++]
    }
    return mat
};

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).