861. Score After Flipping Matrix

Problem

You are given an m x n binary matrix grid.

A move consists of choosing any row or column and toggling each value in that row or column (i.e., changing all 0's to 1's, and all 1's to 0's).

Every row of the matrix is interpreted as a binary number, and the score of the matrix is the sum of these numbers.

Return **the highest possible *score* after making any number of moves (including zero moves)**.

  Example 1:

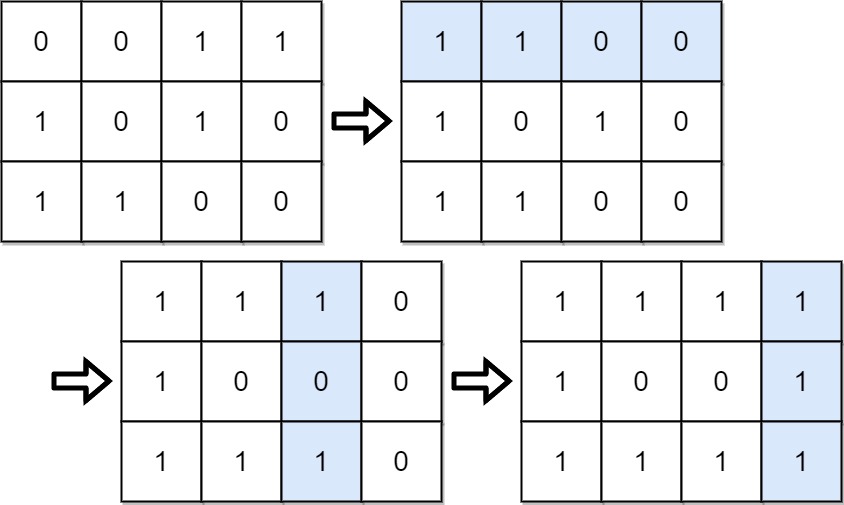
Input: grid = [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
Output: 39
Explanation: 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39

Example 2:

Input: grid = [[0]]
Output: 1

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 20

• grid[i][j] is either 0 or 1.

Solution (Java)

class Solution {
    public int matrixScore(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        for (int i = 0; i < m; i++) {
            if (grid[i][0] == 0) {
                for (int j = 0; j < n; j++) {
                    if (grid[i][j] == 0) {
                        grid[i][j] = 1;
                    } else {
                        grid[i][j] = 0;
                    }
                }
            }
        }
        for (int j = 1; j < n; j++) {
            int ones = 0;
            for (int[] ints : grid) {
                if (ints[j] == 1) {
                    ones++;
                }
            }
            if (ones <= m / 2) {
                for (int i = 0; i < m; i++) {
                    if (grid[i][j] == 1) {
                        grid[i][j] = 0;
                    } else {
                        grid[i][j] = 1;
                    }
                }
            }
        }
        int result = 0;
        for (int[] ints : grid) {
            StringBuilder sb = new StringBuilder();
            for (int j = 0; j < n; j++) {
                sb.append(ints[j]);
            }
            result += Integer.parseInt(sb.toString(), 2);
        }
        return result;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).