850. Rectangle Area II

Problem

You are given a 2D array of axis-aligned rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner.

Calculate the total area covered by all rectangles in the plane. Any area covered by two or more rectangles should only be counted once.

Return **the *total area***. Since the answer may be too large, return it *modulo* 10^9 + 7.

  Example 1:

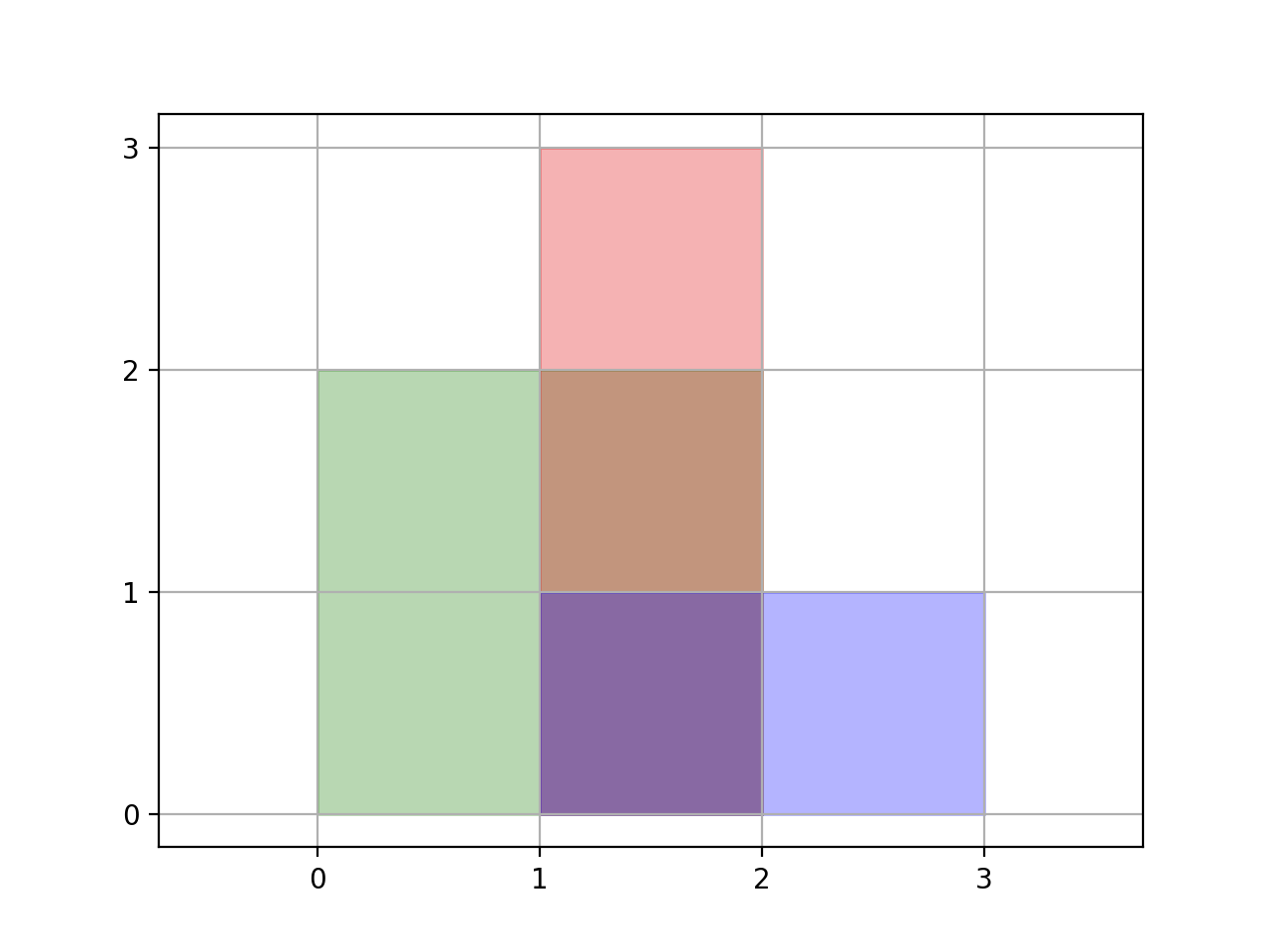
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
Explanation: A total area of 6 is covered by all three rectangles, as illustrated in the picture.
From (1,1) to (2,2), the green and red rectangles overlap.
From (1,0) to (2,3), all three rectangles overlap.

Example 2:

Input: rectangles = [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 1018 modulo (10^9 + 7), which is 49.

  Constraints:

• 1 <= rectangles.length <= 200

• rectanges[i].length == 4

• 0 <= xi1, yi1, xi2, yi2 <= 10^9

Solution

class Solution {
    public int rectangleArea(int[][] rectangles) {
        List<int[]> memo = new ArrayList<>();
        for (int[] rectangle : rectangles) {
            helper(0, rectangle, memo);
        }

        long res = 0;
        final int mod = (int) (1e9 + 7);
        for (int[] m : memo) {
            res = (res + (long) (m[2] - m[0]) * (long) (m[3] - m[1])) % mod;
        }

        return (int) res;
    }

    private void helper(int id, int[] rectangle, List<int[]> memo) {
        if (id >= memo.size()) {
            memo.add(rectangle);
            return;
        }

        int[] cur = memo.get(id);

        if (rectangle[2] <= cur[0]
                || rectangle[0] >= cur[2]
                || rectangle[1] >= cur[3]
                || rectangle[3] <= cur[1]) {
            helper(id + 1, rectangle, memo);
            return;
        }

        if (rectangle[0] < cur[0]) {
            helper(id + 1, new int[] {rectangle[0], rectangle[1], cur[0], rectangle[3]}, memo);
        }

        if (rectangle[2] > cur[2]) {
            helper(id + 1, new int[] {cur[2], rectangle[1], rectangle[2], rectangle[3]}, memo);
        }

        if (rectangle[1] < cur[1]) {
            helper(
                    id + 1,
                    new int[] {
                        Math.max(rectangle[0], cur[0]),
                        rectangle[1],
                        Math.min(rectangle[2], cur[2]),
                        cur[1]
                    },
                    memo);
        }

        if (rectangle[3] > cur[3]) {
            helper(
                    id + 1,
                    new int[] {
                        Math.max(rectangle[0], cur[0]),
                        cur[3],
                        Math.min(rectangle[2], cur[2]),
                        rectangle[3]
                    },
                    memo);
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).