Range Sum Query 2D - Immutable - LeetCode solutions

Problem

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

Example 1:

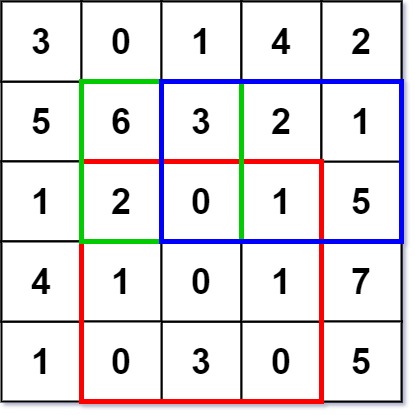
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10^4 <= matrix[i][j] <= 10^4
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10^4 calls will be made to sumRegion.

Solution

class NumMatrix {
    private int[][] tot;

    public NumMatrix(int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return;
        }
        // The dimensions of this tot matrix is actually 1 bigger than the given matrix, cool!
        tot = new int[matrix.length + 1][matrix[0].length + 1];
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                tot[i + 1][j + 1] = matrix[i][j] + tot[i + 1][j] + tot[i][j + 1] - tot[i][j];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        return tot[row2 + 1][col2 + 1]
                - tot[row2 + 1][col1]
                - tot[row1][col2 + 1]
                + tot[row1][col1];
    }
}

/**
 * Your NumMatrix object will be instantiated and called as such:
 * NumMatrix obj = new NumMatrix(matrix);
 * int param_1 = obj.sumRegion(row1,col1,row2,col2);
 */

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).