Problem
You are given an array points where points[i] = [xi, yi] is the coordinates of the ith point on a 2D plane. Multiple points can have the same coordinates.
You are also given an array queries where queries[j] = [xj, yj, rj] describes a circle centered at (xj, yj) with a radius of rj.
For each query queries[j], compute the number of points inside the jth circle. Points on the border of the circle are considered inside.
Return **an array *answer*, where *answer[j]* is the answer to the jth query**.
Example 1:
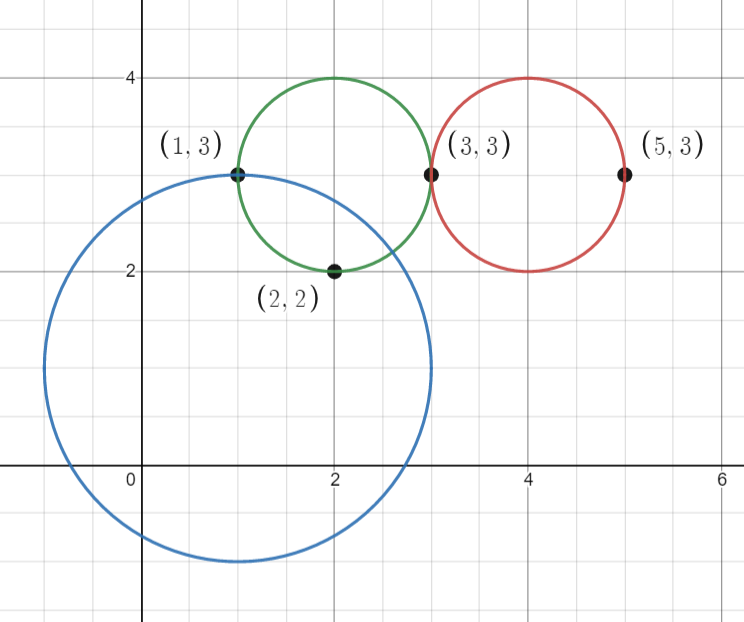
Input: points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
Output: [3,2,2]
Explanation: The points and circles are shown above.
queries[0] is the green circle, queries[1] is the red circle, and queries[2] is the blue circle.
Example 2:
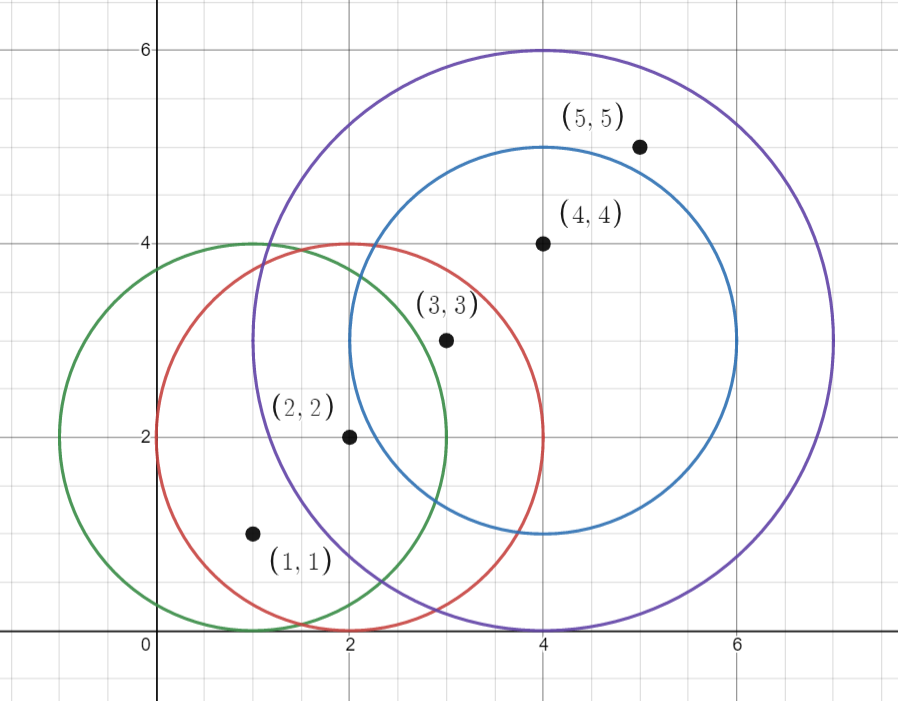
Input: points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
Output: [2,3,2,4]
Explanation: The points and circles are shown above.
queries[0] is green, queries[1] is red, queries[2] is blue, and queries[3] is purple.
Constraints:
1 <= points.length <= 500points[i].length == 20 <= xi, yi <= 5001 <= queries.length <= 500queries[j].length == 30 <= xj, yj <= 5001 <= rj <= 500All coordinates are integers.
Follow up: Could you find the answer for each query in better complexity than O(n)?
Solution (Java)
class Solution {
public int[] countPoints(int[][] points, int[][] queries) {
int[] result = new int[queries.length];
int i = 0;
for (int[] query : queries) {
int pts = 0;
for (int[] point : points) {
if ((point[0] - query[0]) * (point[0] - query[0])
+ (point[1] - query[1]) * (point[1] - query[1])
<= query[2] * query[2]) {
pts++;
}
}
result[i++] = pts;
}
return result;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).