2249. Count Lattice Points Inside a Circle

Problem

Given a 2D integer array circles where circles[i] = [xi, yi, ri] represents the center (xi, yi) and radius ri of the ith circle drawn on a grid, return **the *number of lattice points* ****that are present inside *at least one* circle**.

Note:

• A lattice point is a point with integer coordinates.

• Points that lie on the circumference of a circle are also considered to be inside it.

  Example 1:

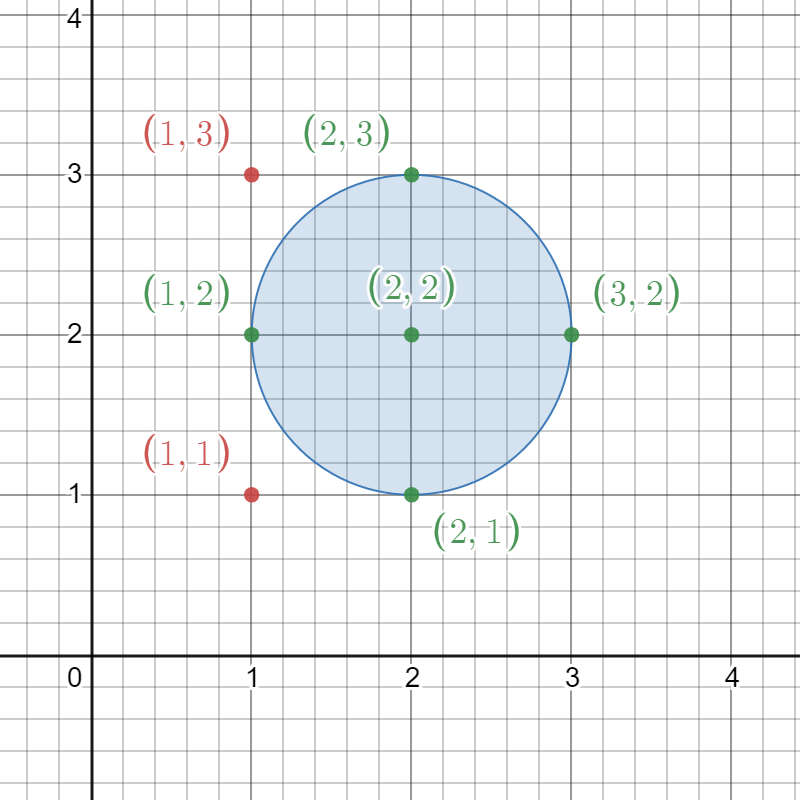
Input: circles = [[2,2,1]]
Output: 5
Explanation:
The figure above shows the given circle.
The lattice points present inside the circle are (1, 2), (2, 1), (2, 2), (2, 3), and (3, 2) and are shown in green.
Other points such as (1, 1) and (1, 3), which are shown in red, are not considered inside the circle.
Hence, the number of lattice points present inside at least one circle is 5.

Example 2:

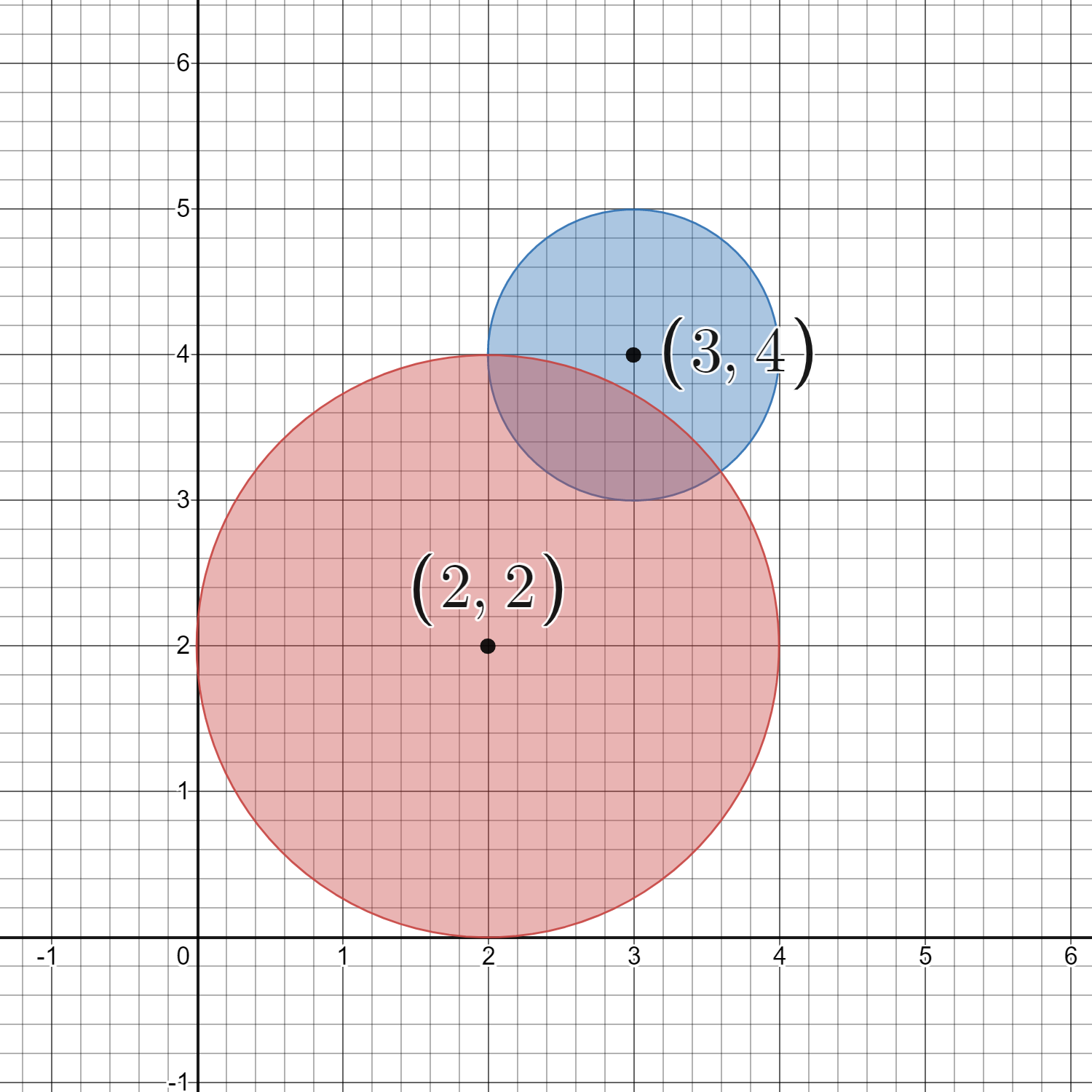
Input: circles = [[2,2,2],[3,4,1]]
Output: 16
Explanation:
The figure above shows the given circles.
There are exactly 16 lattice points which are present inside at least one circle. 
Some of them are (0, 2), (2, 0), (2, 4), (3, 2), and (4, 4).

  Constraints:

• 1 <= circles.length <= 200

• circles[i].length == 3

• 1 <= xi, yi <= 100

• 1 <= ri <= min(xi, yi)

Solution (Java)

class Solution {
    public int countLatticePoints(int[][] circles) {
        int xMin = 200;
        int xMax = -1;
        int yMin = 200;
        int yMax = -1;
        for (int[] c : circles) {
            xMin = Math.min(xMin, c[0] - c[2]);
            xMax = Math.max(xMax, c[0] + c[2]);
            yMin = Math.min(yMin, c[1] - c[2]);
            yMax = Math.max(yMax, c[1] + c[2]);
        }
        int ans = 0;
        for (int x = xMin; x <= xMax; x++) {
            for (int y = yMin; y <= yMax; y++) {
                for (int[] c : circles) {
                    if ((c[0] - x) * (c[0] - x) + (c[1] - y) * (c[1] - y) <= c[2] * c[2]) {
                        ans++;
                        break;
                    }
                }
            }
        }
        return ans;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).