2614. Prime In Diagonal

Problem

You are given a 0-indexed two-dimensional integer array nums.

Return **the largest *prime* number that lies on at least one of the diagonals of nums. In case, no prime is present on any of the diagonals, return 0.**

Note that:

• An integer is prime if it is greater than 1 and has no positive integer divisors other than 1 and itself.
• An integer val is on one of the diagonals of nums if there exists an integer i for which nums[i][i] = val or an i for which nums[i][nums.length - i - 1] = val.

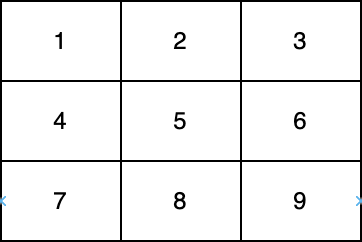
In the above diagram, one diagonal is [1,5,9] and another diagonal is** [3,5,7]**.

Example 1:

Input: nums = [[1,2,3],[5,6,7],[9,10,11]]
Output: 11
Explanation: The numbers 1, 3, 6, 9, and 11 are the only numbers present on at least one of the diagonals. Since 11 is the largest prime, we return 11.

Example 2:

Input: nums = [[1,2,3],[5,17,7],[9,11,10]]
Output: 17
Explanation: The numbers 1, 3, 9, 10, and 17 are all present on at least one of the diagonals. 17 is the largest prime, so we return 17.

Constraints:

• 1 <= nums.length <= 300
• nums.length == numsi.length
• 1 <= nums[i][j]&nbsp;<= 4*106

Solution (Java)

class Solution {
    public int diagonalPrime(int[][] nums) {
        fill();
        int n = nums.length;
        int max = 0;
        for (int i = 0; i < n; i++) {
            if (p[nums[i][i]]) {
                max = Math.max(max, nums[i][i]);
            }
            if (p[nums[i][n - i - 1]]) {
                max = Math.max(max, nums[i][n - i - 1]);
            }
        }
        return max;
    }

    boolean[] p = new boolean[4 * 1000000 + 1];
    private void fill() {
        Arrays.fill(p, true);
        int n = 4 * 1000000;
        for (int i = 2; i * i <= n; i++) {
            if (!p[i]) continue;
            for (int j = 2 * i; j <= n; j += i) {
                p[j] = false;
            }
        }
        p[0] = p[1] = false;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).