2050. Parallel Courses III

Problem

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)th course.

You must find the minimum number of months needed to complete all the courses following these rules:

• You may start taking a course at any time if the prerequisites are met.

• Any number of courses can be taken at the same time.

Return **the *minimum* number of months needed to complete all the courses**.

Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).

  Example 1:

Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
Output: 8
Explanation: The figure above represents the given graph and the time required to complete each course. 
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.

Example 2:

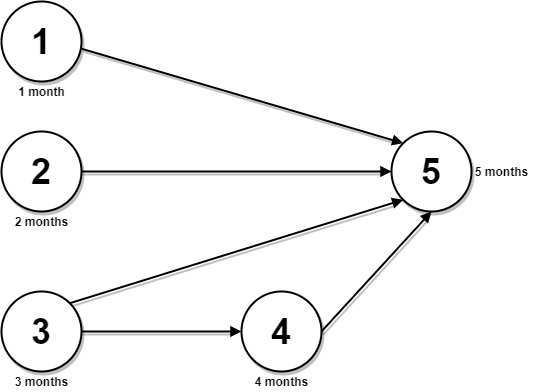
Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
Output: 12
Explanation: The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.

  Constraints:

• 1 <= n <= 5 * 10^4

• 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 10^4)

• relations[j].length == 2

• 1 <= prevCoursej, nextCoursej <= n

• prevCoursej != nextCoursej

• All the pairs [prevCoursej, nextCoursej] are unique.

• time.length == n

• 1 <= time[i] <= 10^4

• The given graph is a directed acyclic graph.

Solution

class Solution {
    public int minimumTime(int n, int[][] relations, int[] time) {
        int v = time.length;
        List<List<Integer>> adj = new ArrayList<>();
        for (int i = 0; i < v; i++) {
            adj.add(new ArrayList<>());
        }
        int[] indegree = new int[v];
        int[] requiredTime = new int[v];
        for (int[] relation : relations) {
            List<Integer> vertices = adj.get(relation[0] - 1);
            vertices.add(relation[1] - 1);
            indegree[relation[1] - 1]++;
        }

        Queue<Integer> q = new ArrayDeque<>();
        for (int i = 0; i < v; i++) {
            if (indegree[i] == 0) {
                q.add(i);
                requiredTime[i] = time[i];
            }
        }

        while (!q.isEmpty()) {
            int vertex = q.poll();
            List<Integer> edges = adj.get(vertex);
            for (Integer e : edges) {
                indegree[e]--;
                if (indegree[e] == 0) {
                    q.add(e);
                }
                int totalTime = time[e] + requiredTime[vertex];
                if (requiredTime[e] < totalTime) {
                    requiredTime[e] = totalTime;
                }
            }
        }
        int maxMonth = 0;
        for (int i = 0; i < n; i++) {
            maxMonth = Math.max(maxMonth, requiredTime[i]);
        }
        return maxMonth;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).