1569. Number of Ways to Reorder Array to Get Same BST

Problem

Given an array nums that represents a permutation of integers from 1 to n. We are going to construct a binary search tree (BST) by inserting the elements of nums in order into an initially empty BST. Find the number of different ways to reorder nums so that the constructed BST is identical to that formed from the original array nums.

• For example, given nums = [2,1,3], we will have 2 as the root, 1 as a left child, and 3 as a right child. The array [2,3,1] also yields the same BST but [3,2,1] yields a different BST.

Return the number of ways to reorder nums such that the BST formed is identical to the original BST formed from nums.

Since the answer may be very large, **return it modulo **10^9 + 7.

  Example 1:

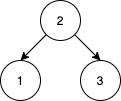
Input: nums = [2,1,3]
Output: 1
Explanation: We can reorder nums to be [2,3,1] which will yield the same BST. There are no other ways to reorder nums which will yield the same BST.

Example 2:

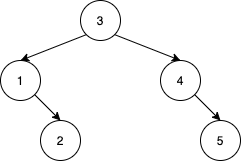
Input: nums = [3,4,5,1,2]
Output: 5
Explanation: The following 5 arrays will yield the same BST: 
[3,1,2,4,5]
[3,1,4,2,5]
[3,1,4,5,2]
[3,4,1,2,5]
[3,4,1,5,2]

Example 3:

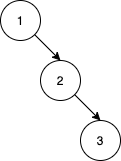
Input: nums = [1,2,3]
Output: 0
Explanation: There are no other orderings of nums that will yield the same BST.

  Constraints:

• 1 <= nums.length <= 1000

• 1 <= nums[i] <= nums.length

• All integers in nums are distinct.

Solution

class Solution {
    public int numOfWays(int[] nums) {
        long mod = 1000000007;
        long[] fact = new long[1001];
        fact[0] = 1;
        for (int i = 1; i <= 1000; i++) {
            fact[i] = (fact[i - 1] * (i)) % mod;
        }
        TreeNode root = new TreeNode(nums[0]);
        for (int i = 1; i < nums.length; i++) {
            addInTree(nums[i], root);
        }

        return (int) ((calcPerms(root, fact).perm - 1) % mod);
    }

    static TreeInfo calcPerms(TreeNode root, long[] fact) {
        TreeInfo left;
        TreeInfo right;

        if (root.left != null) {
            left = calcPerms(root.left, fact);
        } else {
            left = new TreeInfo(0, 1);
        }

        if (root.right != null) {
            right = calcPerms(root.right, fact);
        } else {
            right = new TreeInfo(0, 1);
        }
        long mod = 1000000007;
        long totNodes = left.numOfNodes + right.numOfNodes + 1;

        long modDiv =
                getModDivision(
                        fact[(int) totNodes - 1],
                        fact[(int) left.numOfNodes],
                        fact[(int) right.numOfNodes],
                        mod);
        long perms = (totNodes == 1) ? 1 : ((((left.perm * right.perm) % mod) * modDiv) % mod);

        left.numOfNodes = totNodes;
        left.perm = perms;
        return left;
    }

    static long getModDivision(long a, long b1, long b2, long m) {
        long b = (b1 * b2);

        long inv = getInverse(b, m);
        return ((inv * a) % m);
    }

    static long getInverse(long b, long m) {
        Inverse inv = getInverseExtended(b, m);
        return ((inv.x % m) + m) % m;
    }

    static Inverse getInverseExtended(long a, long b) {
        if (a == 0) {
            return new Inverse(0, 1);
        }

        Inverse inv = getInverseExtended(b % a, a);
        long x1 = inv.y - ((b / a) * inv.x);
        long y1 = inv.x;
        inv.x = x1;
        inv.y = y1;
        return inv;
    }

    static class Inverse {
        long x;
        long y;

        Inverse(long x, long y) {
            this.x = x;
            this.y = y;
        }
    }

    static class TreeInfo {
        long numOfNodes;
        long perm;

        TreeInfo(long numOfNodes, long perm) {
            this.numOfNodes = numOfNodes;
            this.perm = perm;
        }
    }

    static void addInTree(int x, TreeNode root) {
        if (root.val > x) {
            if (root.left != null) {
                addInTree(x, root.left);
            } else {
                root.left = new TreeNode(x);
            }
        }
        if (root.val < x) {
            if (root.right != null) {
                addInTree(x, root.right);
            } else {
                root.right = new TreeNode(x);
            }
        }
    }

    static class TreeNode {
        int val;
        TreeNode left;
        TreeNode right;

        TreeNode(int x) {
            val = x;
            left = null;
            right = null;
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).