1719. Number Of Ways To Reconstruct A Tree

Problem

You are given an array pairs, where pairs[i] = [xi, yi], and:

• There are no duplicates.

• xi < yi

Let ways be the number of rooted trees that satisfy the following conditions:

• The tree consists of nodes whose values appeared in pairs.

• A pair [xi, yi] exists in pairs if and only if xi is an ancestor of yi or yi is an ancestor of xi.

• Note: the tree does not have to be a binary tree.

Two ways are considered to be different if there is at least one node that has different parents in both ways.

Return:

• 0 if ways == 0

• 1 if ways == 1

• 2 if ways > 1

A rooted tree is a tree that has a single root node, and all edges are oriented to be outgoing from the root.

An ancestor of a node is any node on the path from the root to that node (excluding the node itself). The root has no ancestors.

  Example 1:

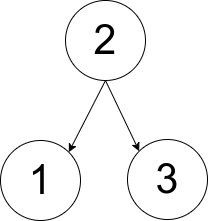
Input: pairs = [[1,2],[2,3]]
Output: 1
Explanation: There is exactly one valid rooted tree, which is shown in the above figure.

Example 2:

Input: pairs = [[1,2],[2,3],[1,3]]
Output: 2
Explanation: There are multiple valid rooted trees. Three of them are shown in the above figures.

Example 3:

Input: pairs = [[1,2],[2,3],[2,4],[1,5]]
Output: 0
Explanation: There are no valid rooted trees.

  Constraints:

• 1 <= pairs.length <= 10^5

• 1 <= xi < yi <= 500

• The elements in pairs are unique.

Solution

class Solution {
    public int checkWays(int[][] pairs) {
        int[][] adj = new int[501][501];
        HashSet<Integer> set = new HashSet<>();
        for (int[] pair : pairs) {
            adj[pair[0]][pair[1]]++;
            adj[pair[1]][pair[0]]++;
            set.add(pair[0]);
            set.add(pair[1]);
        }
        int n = set.size();
        int[] num = new int[501];
        for (int i = 0; i < 501; i++) {
            for (int j = 0; j < 501; j++) {
                num[i] += adj[i][j];
            }
        }
        int c = 0;
        for (int i = 0; i < 501; i++) {
            if (num[i] == n - 1) {
                c++;
            }
        }
        for (int j = 0; j < 501; j++) {
            if (num[j] == n - 1) {
                num[j] = 0;
                for (int k = 0; k < 501; k++) {
                    if (adj[j][k] > 0) {
                        adj[j][k] = 0;
                        adj[k][j] = 0;
                        num[k]--;
                    }
                }
                set.remove(j);
                break;
            }
            if (j == 500) {
                return 0;
            }
        }
        int res = search(adj, num, set);
        if (res == 1 && c > 1) {
            return 2;
        }
        return res;
    }

    private int search(int[][] adj, int[] num, HashSet<Integer> vals) {
        if (vals.isEmpty()) {
            return 1;
        }
        int max = 0;
        for (int i : vals) {
            if (num[i] > num[max]) {
                max = i;
            }
        }
        int size = num[max];
        if (size == 0) {
            return 1;
        }
        boolean c = false;
        i:
        for (int i : vals) {
            if (num[i] == num[max]) {
                for (int j : vals) {
                    if (j != i && num[j] == num[i] && adj[i][j] > 0) {
                        c = true;
                        break i;
                    }
                }
            }
        }
        HashSet<Integer> set = new HashSet<>();
        for (int j = 0; j < 501; j++) {
            if (adj[max][j] > 0 && !vals.contains(j)) {
                return 0;
            }
            if (adj[max][j] > 0) {
                adj[max][j] = 0;
                adj[j][max] = 0;
                num[j]--;
                set.add(j);
            }
        }
        num[max] = 0;
        HashSet<Integer> set2 = new HashSet<>();
        for (int i : vals) {
            if (!set.contains(i) && i != max) {
                set2.add(i);
            }
        }
        int res1 = search(adj, num, set);
        int res2 = search(adj, num, set2);
        if (res1 == 0 || res2 == 0) {
            return 0;
        }
        if (res1 == 2 || res2 == 2 || c) {
            return 2;
        }
        return 1;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).