1786. Number of Restricted Paths From First to Last Node

Problem

There is an undirected weighted connected graph. You are given a positive integer n which denotes that the graph has n nodes labeled from 1 to n, and an array edges where each edges[i] = [ui, vi, weighti] denotes that there is an edge between nodes ui and vi with weight equal to weighti.

A path from node start to node end is a sequence of nodes [z0, z1, z2, ..., zk] such that z0 = start and zk = end and there is an edge between zi and zi+1 where 0 <= i <= k-1.

The distance of a path is the sum of the weights on the edges of the path. Let distanceToLastNode(x) denote the shortest distance of a path between node n and node x. A restricted path is a path that also satisfies that distanceToLastNode(zi) > distanceToLastNode(zi+1) where 0 <= i <= k-1.

Return the number of restricted paths from node 1 to node n. Since that number may be too large, return it modulo 10^9 + 7.

  Example 1:

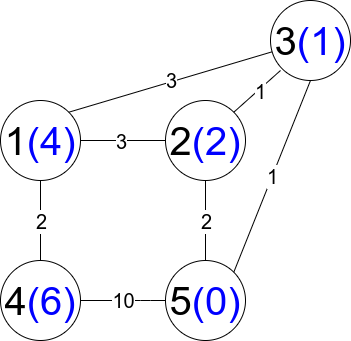
Input: n = 5, edges = [[1,2,3],[1,3,3],[2,3,1],[1,4,2],[5,2,2],[3,5,1],[5,4,10]]
Output: 3
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The three restricted paths are:
1) 1 --> 2 --> 5
2) 1 --> 2 --> 3 --> 5
3) 1 --> 3 --> 5

Example 2:

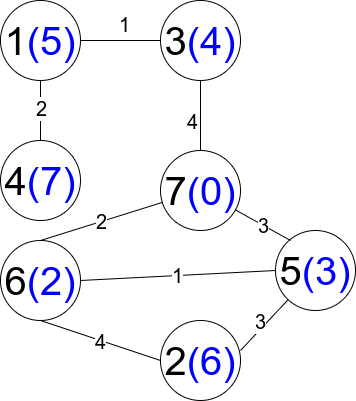
Input: n = 7, edges = [[1,3,1],[4,1,2],[7,3,4],[2,5,3],[5,6,1],[6,7,2],[7,5,3],[2,6,4]]
Output: 1
Explanation: Each circle contains the node number in black and its distanceToLastNode value in blue. The only restricted path is 1 --> 3 --> 7.

  Constraints:

• 1 <= n <= 2 * 10^4

• n - 1 <= edges.length <= 4 * 10^4

• edges[i].length == 3

• 1 <= ui, vi <= n

• ui != vi

• 1 <= weighti <= 10^5

• There is at most one edge between any two nodes.

• There is at least one path between any two nodes.

Solution (Java)

class Solution {
    private static class Pair implements Comparable<Pair> {
        int v;
        int cwt;

        Pair(int v, int cwt) {
            this.v = v;
            this.cwt = cwt;
        }

        public int compareTo(Pair o) {
            return this.cwt - o.cwt;
        }
    }

    private static class Edge {
        int v;
        int wt;

        Edge(int v, int wt) {
            this.v = v;
            this.wt = wt;
        }
    }

    private int[] dtl;
    private int[] dp;
    private static final int M = 1000000007;

    public int countRestrictedPaths(int n, int[][] edges) {
        List<List<Edge>> graph = buildGraph(n, edges);
        PriorityQueue<Pair> pq = new PriorityQueue<>();
        boolean[] vis = new boolean[n + 1];
        dtl = new int[n + 1];
        pq.add(new Pair(n, 0));
        while (!pq.isEmpty()) {
            Pair rem = pq.remove();
            if (vis[rem.v]) {
                continue;
            }
            dtl[rem.v] = rem.cwt;
            vis[rem.v] = true;
            for (Edge edge : graph.get(rem.v)) {
                if (!vis[edge.v]) {
                    pq.add(new Pair(edge.v, rem.cwt + edge.wt));
                }
            }
        }
        dp = new int[n + 1];
        return dfs(graph, 1, new boolean[n + 1], n);
    }

    private int dfs(List<List<Edge>> graph, int vtx, boolean[] vis, int n) {
        if (vtx == n) {
            return 1;
        }
        long ans = 0;
        vis[vtx] = true;
        for (Edge edge : graph.get(vtx)) {
            if (!vis[edge.v] && dtl[edge.v] < dtl[vtx]) {
                int x = dfs(graph, edge.v, vis, n);
                ans = (ans + x) % M;
            } else if (dtl[edge.v] < dtl[vtx] && vis[edge.v]) {
                ans = (ans + dp[edge.v]) % M;
            }
        }
        dp[vtx] = (int) ans;
        return (int) ans;
    }

    private List<List<Edge>> buildGraph(int n, int[][] edges) {
        List<List<Edge>> graph = new ArrayList<>();
        for (int i = 0; i <= n; i++) {
            graph.add(new ArrayList<>());
        }
        for (int[] edge : edges) {
            int u = edge[0];
            int v = edge[1];
            int wt = edge[2];
            graph.get(u).add(new Edge(v, wt));
            graph.get(v).add(new Edge(u, wt));
        }
        return graph;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).