1020. Number of Enclaves

Problem

You are given an m x n binary matrix grid, where 0 represents a sea cell and 1 represents a land cell.

A move consists of walking from one land cell to another adjacent (4-directionally) land cell or walking off the boundary of the grid.

Return the number of land cells in grid **for which we cannot walk off the boundary of the grid in any number of *moves***.

  Example 1:

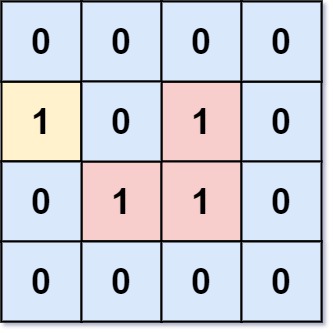
Input: grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
Output: 3
Explanation: There are three 1s that are enclosed by 0s, and one 1 that is not enclosed because its on the boundary.

Example 2:

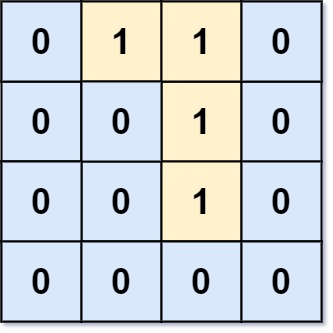
Input: grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
Output: 0
Explanation: All 1s are either on the boundary or can reach the boundary.

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 500

• grid[i][j] is either 0 or 1.

Solution (Java)

class Solution {
    private void walk(int[][] a, boolean[][] visited, int x, int y) {
        if (x >= a.length || x < 0 || y >= a[0].length || y < 0) {
            return;
        }
        if (visited[x][y]) {
            return;
        }
        if (a[x][y] == 0) {
            return;
        }
        visited[x][y] = true;
        walk(a, visited, x - 1, y);
        walk(a, visited, x, y - 1);
        walk(a, visited, x, y + 1);
        walk(a, visited, x + 1, y);
    }

    public int numEnclaves(int[][] a) {
        int n = a.length;
        int m = a[0].length;
        boolean[][] visited = new boolean[n][m];
        for (int i = 0; i < n; ++i) {
            walk(a, visited, i, 0);
            walk(a, visited, i, m - 1);
        }
        for (int j = 0; j < m; ++j) {
            walk(a, visited, 0, j);
            walk(a, visited, n - 1, j);
        }
        int unreachables = 0;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                if (a[i][j] == 1 && !visited[i][j]) {
                    ++unreachables;
                }
            }
        }
        return unreachables;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).