Problem
Given a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.
Return the number of closed islands.
Example 1:
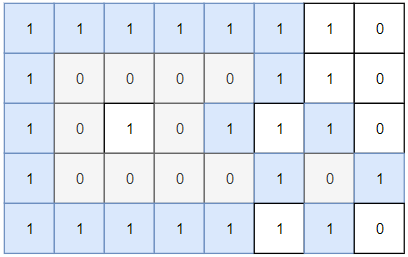
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation:
Islands in gray are closed because they are completely surrounded by water (group of 1s).
Example 2:
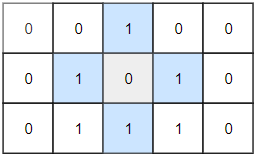
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1
Example 3:
Input: grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
Output: 2
Constraints:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
Solution (Java)
class Solution {
private int rows;
private int cols;
private boolean isLand;
public int closedIsland(int[][] grid) {
rows = grid.length;
cols = grid[0].length;
int result = 0;
for (int r = 0; r < rows; r++) {
for (int c = 0; c < cols; c++) {
if (grid[r][c] == 0) {
isLand = true;
dfs(grid, r, c);
if (isLand) {
result++;
}
}
}
}
return result;
}
private void dfs(int[][] grid, int r, int c) {
if (r == 0 || c == 0 || r == rows - 1 || c == cols - 1) {
isLand = false;
}
grid[r][c] = 'k';
if (r > 0 && grid[r - 1][c] == 0) {
dfs(grid, r - 1, c);
}
if (c > 0 && grid[r][c - 1] == 0) {
dfs(grid, r, c - 1);
}
if (r < rows - 1 && grid[r + 1][c] == 0) {
dfs(grid, r + 1, c);
}
if (c < cols - 1 && grid[r][c + 1] == 0) {
dfs(grid, r, c + 1);
}
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).