Problem
Given the root of a binary tree, return the most frequent subtree sum. If there is a tie, return all the values with the highest frequency in any order.
The subtree sum of a node is defined as the sum of all the node values formed by the subtree rooted at that node (including the node itself).
Example 1:
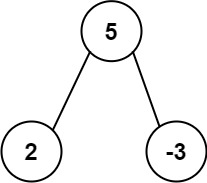
Input: root = [5,2,-3]
Output: [2,-3,4]
Example 2:
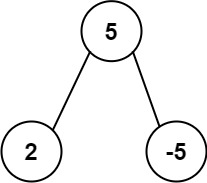
Input: root = [5,2,-5]
Output: [2]
Constraints:
The number of nodes in the tree is in the range
[1, 10^4].-10^5 <= Node.val <= 10^5
Solution (Java)
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int[] findFrequentTreeSum(TreeNode root) {
ArrayList<Integer> arr = new ArrayList<>();
HashMap<Integer, Integer> hm = new HashMap<>();
fun(root, hm);
int maxvalue = Integer.MIN_VALUE;
for (Map.Entry<Integer, Integer> map : hm.entrySet()) {
if (map.getValue() > maxvalue) {
maxvalue = map.getValue();
}
}
for (Map.Entry<Integer, Integer> map : hm.entrySet()) {
if (map.getValue() == maxvalue) {
arr.add(map.getKey());
}
}
int[] newArr = new int[arr.size()];
for (int i = 0; i < arr.size(); i++) {
newArr[i] = arr.get(i);
}
return newArr;
}
private int fun(TreeNode node, HashMap<Integer, Integer> hm) {
if (node == null) {
return 0;
}
int left = fun(node.left, hm);
int right = fun(node.right, hm);
int sum = node.val + left + right;
if (hm.containsKey(sum)) {
hm.put(sum, hm.get(sum) + 1);
} else {
hm.put(sum, 0);
}
return sum;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).