1536. Minimum Swaps to Arrange a Binary Grid

Problem

Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

  Example 1:

Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3

Example 2:

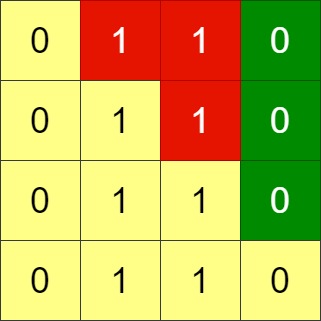
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.

Example 3:

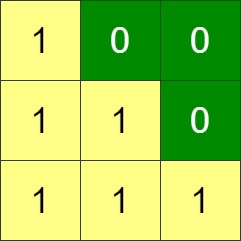
Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0

  Constraints:

• n == grid.length == grid[i].length

• 1 <= n <= 200

• grid[i][j] is either 0 or 1

Solution (Java)

class Solution {
    public int minSwaps(int[][] grid) {
        int len = grid.length;
        int swap = 0;
        int[] preProcess = new int[len];
        for (int i = 0; i < len; i++) {
            preProcess[i] = countRightZeros(grid[i]);
        }
        for (int i = 0; i < len; i++) {
            int minValueRequired = len - i - 1;
            int j = i;
            while (j < len && preProcess[j] < minValueRequired) {
                j++;
            }
            if (j == len) {
                return -1;
            }
            while (j != i) {
                swap++;
                int temp = preProcess[j];
                preProcess[j] = preProcess[j - 1];
                preProcess[j - 1] = temp;
                j--;
            }
        }
        return swap;
    }

    private int countRightZeros(int[] row) {
        int cnt = 0;
        for (int i = row.length - 1; i >= 0; i--) {
            if (row[i] != 0) {
                break;
            }
            cnt++;
        }
        return cnt;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).