2492. Minimum Score of a Path Between Two Cities

Problem

You are given a positive integer n representing n cities numbered from 1 to n. You are also given a 2D array roads where roads[i] = [ai, bi, distancei] indicates that there is a **bidirectional **road between cities ai and bi with a distance equal to distancei. The cities graph is not necessarily connected.

The score of a path between two cities is defined as the **minimum **distance of a road in this path.

Return **the **minimum **possible score of a path between cities *1* and **n.

Note:

• A path is a sequence of roads between two cities.

• It is allowed for a path to contain the same road multiple times, and you can visit cities 1 and n multiple times along the path.

• The test cases are generated such that there is at least one path between 1 and n.

  Example 1:

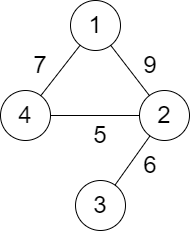
Input: n = 4, roads = [[1,2,9],[2,3,6],[2,4,5],[1,4,7]]
Output: 5
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 4. The score of this path is min(9,5) = 5.
It can be shown that no other path has less score.

Example 2:

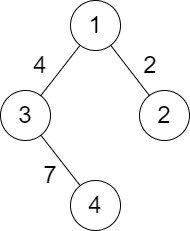
Input: n = 4, roads = [[1,2,2],[1,3,4],[3,4,7]]
Output: 2
Explanation: The path from city 1 to 4 with the minimum score is: 1 -> 2 -> 1 -> 3 -> 4. The score of this path is min(2,2,4,7) = 2.

  Constraints:

• 2 <= n <= 105

• 1 <= roads.length <= 105

• roads[i].length == 3

• 1 <= ai, bi <= n

• ai != bi

• 1 <= distancei <= 104

• There are no repeated edges.

• There is at least one path between 1 and n.

Solution (Java)

class Solution {
    public int minScore(int n, int[][] roads) {
        HashMap<Integer, HashMap<Integer, Integer>>graph = new HashMap<Integer, HashMap<Integer, Integer>>();
        for(int i = 1; i <= n; i++){
            graph.put(i, new HashMap<Integer, Integer>());
        }
        for(int i = 0; i < roads.length; i++){
            int src = roads[i][0];
            int dest = roads[i][1];
            int dist = roads[i][2];
            graph.get(src).put(dest, dist);
            graph.get(dest).put(src, dist);
        }
        HashSet<Integer>visited = new HashSet<Integer>();
        return minDistanceOfConnectedNode(graph, visited, 1, n);
    }
    private int minDistanceOfConnectedNode(HashMap<Integer, HashMap<Integer, Integer>>graph, HashSet<Integer>visited, int start, int end){
        Queue<Integer> queue = new LinkedList<Integer>();
        queue.add(start);
        visited.add(start);
        int min = Integer.MAX_VALUE;
        while(!queue.isEmpty()){
            int size = queue.size();
            for(int i = 0; i < size; i++){
                int top = queue.remove();
                for(int child : graph.get(top).keySet()){
                    min = Math.min(graph.get(top).get(child), min);
                    if(!visited.contains(child)){
                        visited.add(child);
                        queue.add(child);
                    }
                }
            }
        }
        return min;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).