Problem
An undirected graph of n nodes is defined by edgeList, where edgeList[i] = [ui, vi, disi] denotes an edge between nodes ui and vi with distance disi. Note that there may be multiple edges between two nodes.
Given an array queries, where queries[j] = [pj, qj, limitj], your task is to determine for each queries[j] whether there is a path between pj and qj such that each edge on the path has a distance strictly less than limitj .
Return **a *boolean array* answer, where **answer.length == queries.length **and the **jth **value of **answer *is true if there is a path for queries[j] is true, and false otherwise*.
Example 1:
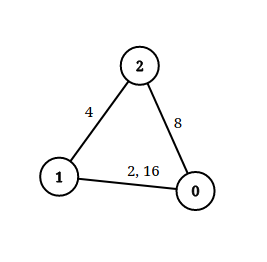
Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
Output: [false,true]
Explanation: The above figure shows the given graph. Note that there are two overlapping edges between 0 and 1 with distances 2 and 16.
For the first query, between 0 and 1 there is no path where each distance is less than 2, thus we return false for this query.
For the second query, there is a path (0 -> 1 -> 2) of two edges with distances less than 5, thus we return true for this query.
Example 2:
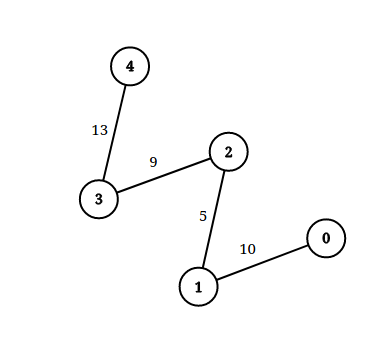
Input: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
Output: [true,false]
Exaplanation: The above figure shows the given graph.
Constraints:
2 <= n <= 10^51 <= edgeList.length, queries.length <= 10^5edgeList[i].length == 3queries[j].length == 30 <= ui, vi, pj, qj <= n - 1ui != vipj != qj1 <= disi, limitj <= 10^9There may be multiple edges between two nodes.
Solution
class Solution {
private static class Dsu {
private int[] parent;
public Dsu(int n) {
parent = new int[n];
Arrays.fill(parent, -1);
}
public int find(int num) {
if (parent[num] == -1) {
return num;
}
parent[num] = find(parent[num]);
return parent[num];
}
public void union(int a, int b) {
int p1 = find(a);
int p2 = find(b);
if (p1 != p2) {
parent[p2] = p1;
}
}
}
public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {
Arrays.sort(edgeList, (o1, o2) -> Integer.compare(o1[2], o2[2]));
int[][] data = new int[queries.length][4];
for (int i = 0; i < queries.length; i++) {
data[i] = new int[] {queries[i][0], queries[i][1], queries[i][2], i};
}
Arrays.sort(data, (o1, o2) -> Integer.compare(o1[2], o2[2]));
Dsu d = new Dsu(n);
int j = 0;
boolean[] ans = new boolean[queries.length];
for (int[] datum : data) {
while (j < edgeList.length && edgeList[j][2] < datum[2]) {
d.union(edgeList[j][0], edgeList[j][1]);
j++;
}
if (d.find(datum[0]) == d.find(datum[1])) {
ans[datum[3]] = true;
}
}
return ans;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).