Minimum Possible Integer After at Most K Adjacent Swaps On Digits

Problem

You are given a string num representing the digits of a very large integer and an integer k. You are allowed to swap any two adjacent digits of the integer at most k times.

Return the minimum integer you can obtain also as a string.

Example 1:

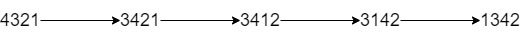
Input: num = "4321", k = 4
Output: "1342"
Explanation: The steps to obtain the minimum integer from 4321 with 4 adjacent swaps are shown.

Example 2:

Input: num = "100", k = 1
Output: "010"
Explanation: It's ok for the output to have leading zeros, but the input is guaranteed not to have any leading zeros.

Example 3:

Input: num = "36789", k = 1000
Output: "36789"
Explanation: We can keep the number without any swaps.

Constraints:

1 <= num.length <= 3 * 10^4
num consists of only digits and does not contain leading zeros.
1 <= k <= 10^9

Solution

class Solution {
    public String minInteger(String num, int k) {
        StringBuilder sb = new StringBuilder();
        int[] digitPos = new int[10];
        int[] reduceMove = new int[10];
        int matchAmount = 0;
        char[] chars = num.toCharArray();
        Arrays.fill(digitPos, chars.length);
        for (int i = 0; i < chars.length; i++) {
            int cur = chars[i] - '0';
            if (digitPos[cur] == chars.length) {
                digitPos[cur] = i;
                matchAmount++;
                if (matchAmount == 10) {
                    break;
                }
            }
        }
        int curIndex = 0;
        while (k > 0 && curIndex < chars.length) {
            for (int digit = 0; digit <= 9; digit++) {
                if (digitPos[digit] < chars.length && digitPos[digit] - reduceMove[digit] <= k) {
                    sb.append(chars[digitPos[digit]]);
                    k -= (digitPos[digit] - reduceMove[digit]);
                    curIndex++;
                    reduceMove[digit]++;
                    for (int j = 0; j <= 9; j++) {
                        if (j != digit && digitPos[j] > digitPos[digit]) {
                            reduceMove[j]++;
                        }
                    }
                    boolean find = false;
                    for (int next = digitPos[digit] + 1; next < chars.length; next++) {
                        int cur = chars[next] - '0';
                        if (cur == digit) {
                            find = true;
                            digitPos[digit] = next;
                            break;
                        }
                        if (next < digitPos[cur]) {
                            reduceMove[digit]++;
                        }
                    }
                    if (!find) {
                        digitPos[digit] = chars.length;
                    }
                    break;
                }
            }
        }
        int start = Arrays.stream(digitPos).min().getAsInt();
        for (int i = start; i < chars.length; i++) {
            if (digitPos[chars[i] - '0'] <= i) {
                sb.append(chars[i]);
            }
        }
        return sb.toString();
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).