2033. Minimum Operations to Make a Uni-Value Grid

Problem

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return **the *minimum* number of operations to make the grid uni-value**. If it is not possible, return -1.

  Example 1:

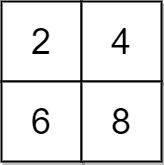
Input: grid = [[2,4],[6,8]], x = 2
Output: 4
Explanation: We can make every element equal to 4 by doing the following: 
- Add x to 2 once.
- Subtract x from 6 once.
- Subtract x from 8 twice.
A total of 4 operations were used.

Example 2:

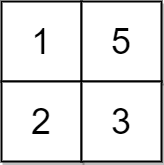
Input: grid = [[1,5],[2,3]], x = 1
Output: 5
Explanation: We can make every element equal to 3.

Example 3:

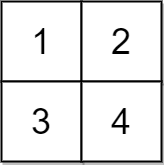
Input: grid = [[1,2],[3,4]], x = 2
Output: -1
Explanation: It is impossible to make every element equal.

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 10^5

• 1 <= m * n <= 10^5

• 1 <= x, grid[i][j] <= 10^4

Solution (Java)

class Solution {
    public int minOperations(int[][] grid, int x) {
        int[] arr = new int[grid.length * grid[0].length];
        int k = 0;
        for (int[] ints : grid) {
            for (int j = 0; j < grid[0].length; j++) {
                arr[k] = ints[j];
                k++;
            }
        }
        Arrays.sort(arr);
        int target = arr[arr.length / 2];
        int res = 0;
        for (int i = 0; i < arr.length; i++) {
            if (i < arr.length / 2) {
                int rem = target - arr[i];
                if (rem % x != 0) {
                    return -1;
                }
                res += rem / x;
            } else {
                int rem = arr[i] - target;
                if (rem % x != 0) {
                    return -1;
                }
                res += rem / x;
            }
        }
        return res;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).