2290. Minimum Obstacle Removal to Reach Corner

Problem

You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:

• 0 represents an empty cell,

• 1 represents an obstacle that may be removed.

You can move up, down, left, or right from and to an empty cell.

Return **the *minimum* number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner **(m - 1, n - 1).

  Example 1:

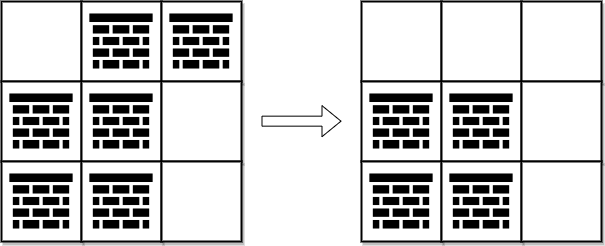
Input: grid = [[0,1,1],[1,1,0],[1,1,0]]
Output: 2
Explanation: We can remove the obstacles at (0, 1) and (0, 2) to create a path from (0, 0) to (2, 2).
It can be shown that we need to remove at least 2 obstacles, so we return 2.
Note that there may be other ways to remove 2 obstacles to create a path.

Example 2:

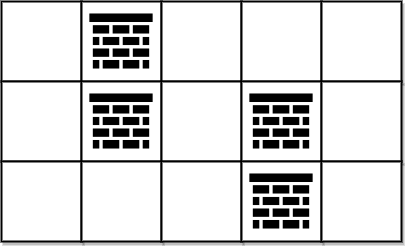
Input: grid = [[0,1,0,0,0],[0,1,0,1,0],[0,0,0,1,0]]
Output: 0
Explanation: We can move from (0, 0) to (2, 4) without removing any obstacles, so we return 0.

  Constraints:

• m == grid.length

• n == grid[i].length

• 1 <= m, n <= 10^5

• 2 <= m * n <= 10^5

• grid[i][j] is either 0 or 1.

• grid[0][0] == grid[m - 1][n - 1] == 0

Solution

class Solution {
    public int minimumObstacles(int[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        int[][] dirs = new int[][] {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
        Queue<State> q = new PriorityQueue<>((a, b) -> a.removed - b.removed);
        q.add(new State(0, 0, 0));
        boolean[][] visited = new boolean[n][m];
        visited[0][0] = true;
        while (!q.isEmpty()) {
            State state = q.poll();
            if (state.r == n - 1 && state.c == m - 1) {
                return state.removed;
            }
            for (int[] d : dirs) {
                int nr = state.r + d[0];
                int nc = state.c + d[1];
                if (nr < 0 || nc < 0 || nr == n || nc == m || visited[nr][nc]) {
                    continue;
                }
                visited[nr][nc] = true;
                State next = new State(nr, nc, state.removed);
                if (grid[nr][nc] == 1) {
                    next.removed++;
                }
                q.add(next);
            }
        }
        return -1;
    }

    private static class State {
        int r;
        int c;
        int removed;

        State(int r, int c, int removed) {
            this.r = r;
            this.c = c;
            this.removed = removed;
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).