2617. Minimum Number of Visited Cells in a Grid

Problem

You are given a 0-indexed m x n integer matrix grid. Your initial position is at the top-left cell (0, 0).

Starting from the cell (i, j), you can move to one of the following cells:

• Cells (i, k) with j < k <= grid[i][j] + j (rightward movement), or
• Cells (k, j) with i < k <= grid[i][j] + i (downward movement).

Return **the minimum number of cells you need to visit to reach the *bottom-right* cell** (m - 1, n - 1). If there is no valid path, return -1.

Example 1:

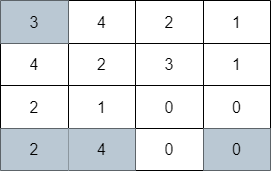
Input: grid = [[3,4,2,1],[4,2,3,1],[2,1,0,0],[2,4,0,0]]
Output: 4
Explanation: The image above shows one of the paths that visits exactly 4 cells.

Example 2:

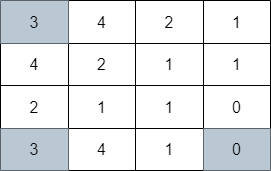
Input: grid = [[3,4,2,1],[4,2,1,1],[2,1,1,0],[3,4,1,0]]
Output: 3
Explanation: The image above shows one of the paths that visits exactly 3 cells.

Example 3:

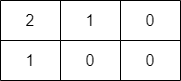
Input: grid = [[2,1,0],[1,0,0]]
Output: -1
Explanation: It can be proven that no path exists.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 0 <= grid[i][j] < m * n
• grid[m - 1][n - 1] == 0

Solution (Java)

class Solution {
    public int minimumVisitedCells(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        boolean[][] visited = new boolean[m][n];
        int[] horizontals = new int[m], verticals = new int[n];
        LinkedList<int[]> queue = new LinkedList<>();
        queue.add(new int[] {0, 0});
        horizontals[0] = 1;
        verticals[0] = 1;
        for (int output = 1; !queue.isEmpty(); output++) for (int i = queue.size(); i > 0; i--) {
            int[] t = queue.removeFirst();
            int x = t[0], y = t[1];
            if (x == m - 1 && y == n - 1) return output;
            for (int j = Math.max(horizontals[x], y + 1); j <= grid[x][y] + y && j < n; j++) if (!visited[x][j]) {
                visited[x][j] = true;
                queue.add(new int[] {x, j});
            }
            while (horizontals[x] < n && visited[x][horizontals[x]]) horizontals[x]++;
            for (int j = Math.max(verticals[y], x + 1); j <= grid[x][y] + x && j < m; j++) if (!visited[j][y]) {
                visited[j][y] = true;
                queue.add(new int[] {j, y});
            }
            while (verticals[y] < m && visited[verticals[y]][y]) verticals[y]++;
        }
        return -1;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).