Problem
There is an undirected tree with n nodes labeled from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates that there is an edge between nodes ui and vi with weight wi in the tree.
You are also given a 2D integer array queries of length m, where queries[i] = [ai, bi]. For each query, find the minimum number of operations required to make the weight of every edge on the path from ai to bi equal. In one operation, you can choose any edge of the tree and change its weight to any value.
Note that:
- Queries are independent of each other, meaning that the tree returns to its initial state on each new query.
- The path from
aitobiis a sequence of distinct nodes starting with nodeaiand ending with nodebisuch that every two adjacent nodes in the sequence share an edge in the tree.
Return **an array *answer* of length m where** answer[i] is the answer to the ith query.
Example 1:
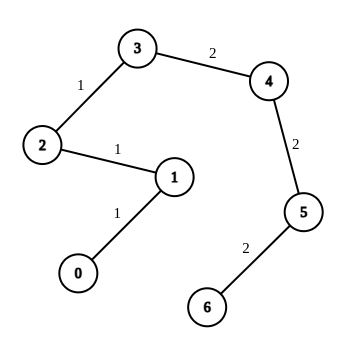
Input: n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
Output: [0,0,1,3]
Explanation: In the first query, all the edges in the path from 0 to 3 have a weight of 1. Hence, the answer is 0.
In the second query, all the edges in the path from 3 to 6 have a weight of 2. Hence, the answer is 0.
In the third query, we change the weight of edge [2,3] to 2. After this operation, all the edges in the path from 2 to 6 have a weight of 2. Hence, the answer is 1.
In the fourth query, we change the weights of edges [0,1], [1,2] and [2,3] to 2. After these operations, all the edges in the path from 0 to 6 have a weight of 2. Hence, the answer is 3.
For each queries[i], it can be shown that answer[i] is the minimum number of operations needed to equalize all the edge weights in the path from ai to bi.
Example 2:
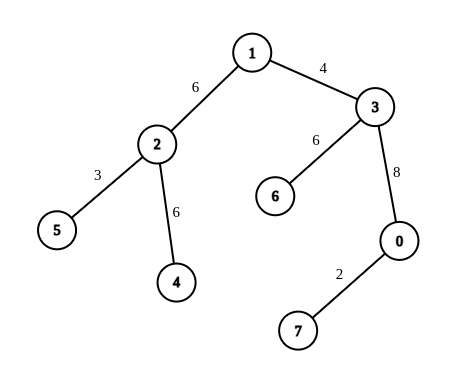
Input: n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
Output: [1,2,2,3]
Explanation: In the first query, we change the weight of edge [1,3] to 6. After this operation, all the edges in the path from 4 to 6 have a weight of 6. Hence, the answer is 1.
In the second query, we change the weight of edges [0,3] and [3,1] to 6. After these operations, all the edges in the path from 0 to 4 have a weight of 6. Hence, the answer is 2.
In the third query, we change the weight of edges [1,3] and [5,2] to 6. After these operations, all the edges in the path from 6 to 5 have a weight of 6. Hence, the answer is 2.
In the fourth query, we change the weights of edges [0,7], [0,3] and [1,3] to 6. After these operations, all the edges in the path from 7 to 4 have a weight of 6. Hence, the answer is 3.
For each queries[i], it can be shown that answer[i] is the minimum number of operations needed to equalize all the edge weights in the path from ai to bi.
Constraints:
1 <= n <= 104edges.length == n - 1edges[i].length == 30 <= ui, vi < n1 <= wi <= 26- The input is generated such that
edgesrepresents a valid tree. 1 <= queries.length == m <= 2 * 104queries[i].length == 20 <= ai, bi < n
Solution (Java)
class Solution {
public void dfs(int x, int f, int dep, List<Pair<Integer, Integer>> []g, int [][]fa, int [][]w, int []d) {
fa[0][x] = f;
d[x] = dep;
for (Pair<Integer, Integer> p: g[x]) {
//Pair<Integer, Integer> p = g[x].get(i);
int c = p.getKey().intValue(), weight = p.getValue().intValue();
if (f == c) continue;
for (int j = 0; j < w[c].length; ++j)
w[c][j] = w[x][j];
w[c][weight]++;
dfs(c, x, dep + 1, g, fa, w, d);
}
}
public int lca(int x, int y, int [][]fa, int []d) {
int m = fa.length;
if (d[x] > d[y]) {
int t = x;
x = y;
y = t;
}
// adjust x and y to the same depth:
for (int p = 0; (1 << p) <= d[y] - d[x]; ++p) {
if (((1 << p) & d[y] - d[x]) != 0) {
y = fa[p][y];
}
}
// conservatively jump x and y together, until they meet:
for (int p = m - 1; p >= 0; --p) {
if (fa[p][x] != fa[p][y]) {
x = fa[p][x];
y = fa[p][y];
}
}
return x == y ? x : fa[0][x];
}
public int[] minOperationsQueries(int n, int[][] edges, int[][] queries) {
int m = 15, C = 27;
List<Pair<Integer, Integer>> []g = new ArrayList[n];
for (int i = 0; i < n; ++i)
g[i] = new ArrayList<Pair<Integer, Integer>>();
for (int[] e : edges) {
g[e[0]].add(new Pair<Integer, Integer>(e[1], e[2]));
g[e[1]].add(new Pair<Integer, Integer>(e[0], e[2]));
}
// fa[i][j] means the 2^i -th father of vertex j:
int [][]fa = new int[m][n];
// w[i][j] means the count of j from root to vertex i:
int [][]w = new int[n][C];
// d[i] means the depth of vertex i:
int []d = new int[n];
dfs(0, 0, 0, g, fa, w, d);
// binary lifting:
for (int i = 1; i < m; ++i) {
for (int j = 0; j < n; ++j) {
fa[i][j] = fa[i-1][fa[i-1][j]];
}
}
int []res = new int[queries.length];
for (int i = 0; i < queries.length; ++i) {
int x = queries[i][0], y = queries[i][1], l = lca(x, y, fa, d);
// the total length between x and y:
int len = d[x] + d[y] - 2 * d[l];
// the mode of weight between x and y:
int max_z = 0;
for (int z = 1; z < C; ++z) {
int num_z = w[x][z] + w[y][z] - w[l][z] * 2;
max_z = Math.max(max_z, num_z);
}
// the others must be changed:
res[i] = len - max_z;
}
return res;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).