Problem
You are given two groups of points where the first group has size1 points, the second group has size2 points, and size1 >= size2.
The cost of the connection between any two points are given in an size1 x size2 matrix where cost[i][j] is the cost of connecting point i of the first group and point j of the second group. The groups are connected if each point in both groups is connected to one or more points in the opposite group. In other words, each point in the first group must be connected to at least one point in the second group, and each point in the second group must be connected to at least one point in the first group.
Return the minimum cost it takes to connect the two groups.
Example 1:
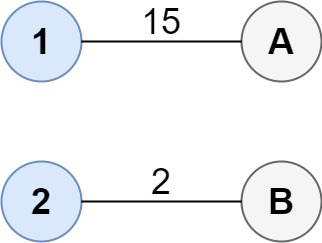
Input: cost = [[15, 96], [36, 2]]
Output: 17
Explanation: The optimal way of connecting the groups is:
1--A
2--B
This results in a total cost of 17.
Example 2:
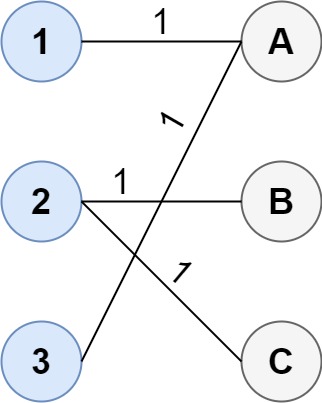
Input: cost = [[1, 3, 5], [4, 1, 1], [1, 5, 3]]
Output: 4
Explanation: The optimal way of connecting the groups is:
1--A
2--B
2--C
3--A
This results in a total cost of 4.
Note that there are multiple points connected to point 2 in the first group and point A in the second group. This does not matter as there is no limit to the number of points that can be connected. We only care about the minimum total cost.
Example 3:
Input: cost = [[2, 5, 1], [3, 4, 7], [8, 1, 2], [6, 2, 4], [3, 8, 8]]
Output: 10
Constraints:
size1 == cost.lengthsize2 == cost[i].length1 <= size1, size2 <= 12size1 >= size20 <= cost[i][j] <= 100
Solution
class Solution {
public int connectTwoGroups(List<List<Integer>> cost) {
// size of set 1
int m = cost.size();
// size of set 2
int n = cost.get(0).size();
int mask = 1 << m;
// min cost to connect nodes in set 1 (of different states);
int[] record = new int[mask];
Arrays.fill(record, Integer.MAX_VALUE);
// since we use record to get the min cost of connecting nodes in set 1
// we shall go through nodes in set 2 one by one, to make sure they are connected
// base case:
record[0] = 0;
for (int col = 0; col < n; col++) {
int[] tmpRecord = new int[mask];
Arrays.fill(tmpRecord, Integer.MAX_VALUE);
// try connection with each of the node in set 1
for (int row = 0; row < m; row++) {
for (int msk = 0; msk < mask; msk++) {
// the new min cost should be based on the cost record of connecting previous
// node in set 2;
int newMask = msk | (1 << row);
if (record[msk] != Integer.MAX_VALUE) {
tmpRecord[newMask] =
Math.min(tmpRecord[newMask], record[msk] + cost.get(row).get(col));
}
// if row nodes in this state has not been connected yet, and the msk is
// achievable by connecting the current node
// then check whether connect the current node multiple times will benefit the
// cost
if ((msk & (1 << row)) == 0 && tmpRecord[msk] != Integer.MAX_VALUE) {
tmpRecord[newMask] =
Math.min(
tmpRecord[newMask],
tmpRecord[msk] + cost.get(row).get(col));
}
}
}
// use tmpRecord to update record
record = tmpRecord;
}
return record[(1 << m) - 1];
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).