2497. Maximum Star Sum of a Graph

Problem

There is an undirected graph consisting of n nodes numbered from 0 to n - 1. You are given a 0-indexed integer array vals of length n where vals[i] denotes the value of the ith node.

You are also given a 2D integer array edges where edges[i] = [ai, bi] denotes that there exists an undirected edge connecting nodes ai and bi.

A star graph is a subgraph of the given graph having a center node containing 0 or more neighbors. In other words, it is a subset of edges of the given graph such that there exists a common node for all edges.

The image below shows star graphs with 3 and 4 neighbors respectively, centered at the blue node.

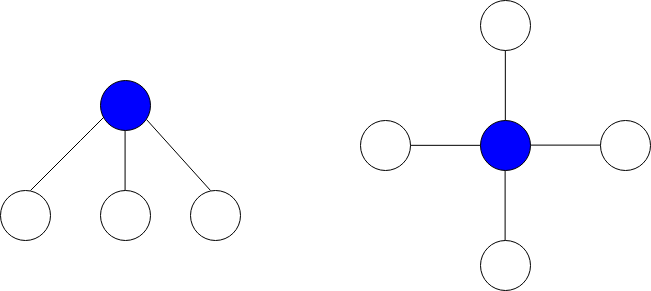
The star sum is the sum of the values of all the nodes present in the star graph.

Given an integer k, return **the *maximum star sum* of a star graph containing at most k edges.**

  Example 1:

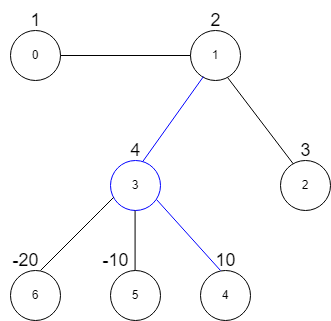
Input: vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2
Output: 16
Explanation: The above diagram represents the input graph.
The star graph with the maximum star sum is denoted by blue. It is centered at 3 and includes its neighbors 1 and 4.
It can be shown it is not possible to get a star graph with a sum greater than 16.

Example 2:

Input: vals = [-5], edges = [], k = 0
Output: -5
Explanation: There is only one possible star graph, which is node 0 itself.
Hence, we return -5.

  Constraints:

• n == vals.length

• 1 <= n <= 105

• -104 <= vals[i] <= 104

• 0 <= edges.length <= min(n * (n - 1) / 2, 105)

• edges[i].length == 2

• 0 <= ai, bi <= n - 1

• ai != bi

• 0 <= k <= n - 1

Solution (Java)

class Solution {
  public int maxStarSum(int[] vals, int[][] edges, int k) {
    Map<Integer, Queue<Integer>> graph = new HashMap<>();
    for (int[] edge : edges) {
      graph.putIfAbsent(edge[0], new PriorityQueue<>());
      if (vals[edge[1]] > 0) {
        Queue<Integer> queue = graph.get(edge[0]);
        queue.offer(vals[edge[1]]);
        if (queue.size() > k) {
          queue.poll();
        }
      }

      graph.putIfAbsent(edge[1], new PriorityQueue<>());
      if (vals[edge[0]] > 0) {
        Queue<Integer> queue = graph.get(edge[1]);
        queue.offer(vals[edge[0]]);
        if (queue.size() > k) {
          queue.poll();
        }
      }
    }

    int result = Integer.MIN_VALUE;
    // for lack of edge case
    for(int star: vals) {
      result = Math.max(result, star);
    }

    for (Map.Entry<Integer, Queue<Integer>> entry : graph.entrySet()) {
      int sum = vals[entry.getKey()];
      for (int star : entry.getValue()) {
        sum += star;
      }

      result = Math.max(result, sum);
    }

    return result;
  }
}

Explain:

nope.

Complexity:

• Time complexity : O(N * log N).
• Space complexity : O(N).