1292. Maximum Side Length of a Square with Sum Less than or Equal to Threshold

Problem

Given a m x n matrix mat and an integer threshold, return **the maximum side-length of a square with a sum less than or equal to *threshold* or return 0 if there is no such square**.

  Example 1:

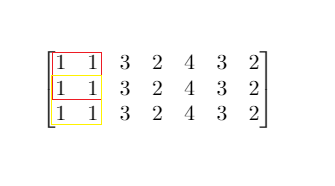
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

  Constraints:

• m == mat.length

• n == mat[i].length

• 1 <= m, n <= 300

• 0 <= mat[i][j] <= 10^4

• 0 <= threshold <= 10^5

Solution (Java)

class Solution {
    public int maxSideLength(int[][] mat, int threshold) {
        int m = mat.length;
        int n = mat[0].length;
        int[][] prefix = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (i == 0 && j == 0) {
                    prefix[i][j] = mat[i][j];
                } else if (i == 0) {
                    prefix[i][j] = mat[i][j] + prefix[0][j - 1];
                } else if (j == 0) {
                    prefix[i][j] = mat[i][j] + prefix[i - 1][0];
                } else {
                    prefix[i][j] =
                            mat[i][j] + prefix[i][j - 1] + prefix[i - 1][j] - prefix[i - 1][j - 1];
                }
            }
        }
        int low = 1;
        int high = Math.min(m, n);
        int ans = 0;
        while (low <= high) {
            int mid = (low + high) / 2;
            if (min(mid, prefix) > threshold) {
                high = mid - 1;
            } else {
                ans = mid;
                low = mid + 1;
            }
        }
        return ans;
    }

    int min(int length, int[][] prefix) {
        int min = 0;
        for (int i = length - 1; i < prefix.length; i++) {
            for (int j = length - 1; j < prefix[0].length; j++) {
                if (i == length - 1 && j == length - 1) {
                    min = prefix[i][j];
                } else if (i - length < 0) {
                    min = Math.min(min, prefix[i][j] - prefix[i][j - length]);
                } else if (j - length < 0) {
                    min = Math.min(min, prefix[i][j] - prefix[i - length][j]);
                } else {
                    min =
                            Math.min(
                                    min,
                                    prefix[i][j]
                                            - prefix[i][j - length]
                                            - prefix[i - length][j]
                                            + prefix[i - length][j - length]);
                }
            }
        }
        return min;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).