2141. Maximum Running Time of N Computers

Problem

You have n computers. You are given the integer n and a 0-indexed integer array batteries where the ith battery can run a computer for batteries[i] minutes. You are interested in running all n computers simultaneously using the given batteries.

Initially, you can insert at most one battery into each computer. After that and at any integer time moment, you can remove a battery from a computer and insert another battery any number of times. The inserted battery can be a totally new battery or a battery from another computer. You may assume that the removing and inserting processes take no time.

Note that the batteries cannot be recharged.

Return **the *maximum* number of minutes you can run all the n computers simultaneously.**

  Example 1:

Input: n = 2, batteries = [3,3,3]
Output: 4
Explanation: 
Initially, insert battery 0 into the first computer and battery 1 into the second computer.
After two minutes, remove battery 1 from the second computer and insert battery 2 instead. Note that battery 1 can still run for one minute.
At the end of the third minute, battery 0 is drained, and you need to remove it from the first computer and insert battery 1 instead.
By the end of the fourth minute, battery 1 is also drained, and the first computer is no longer running.
We can run the two computers simultaneously for at most 4 minutes, so we return 4.

Example 2:

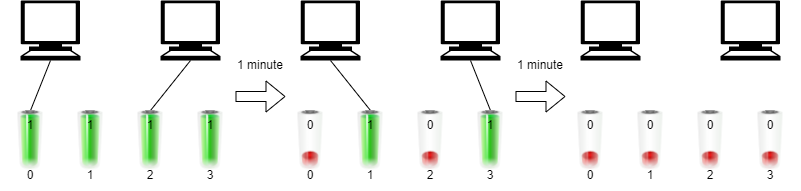
Input: n = 2, batteries = [1,1,1,1]
Output: 2
Explanation: 
Initially, insert battery 0 into the first computer and battery 2 into the second computer. 
After one minute, battery 0 and battery 2 are drained so you need to remove them and insert battery 1 into the first computer and battery 3 into the second computer. 
After another minute, battery 1 and battery 3 are also drained so the first and second computers are no longer running.
We can run the two computers simultaneously for at most 2 minutes, so we return 2.

  Constraints:

• 1 <= n <= batteries.length <= 10^5

• 1 <= batteries[i] <= 10^9

Solution

class Solution {
    private boolean isPossibeToRun(int n, int[] batteries, long avgTime) {
        long duration = 0;
        for (long ele : batteries) {
            duration += Math.min(ele, avgTime);
        }
        return avgTime * n <= duration;
    }

    public long maxRunTime(int n, int[] batteries) {
        long startTime = 0;
        long sum = 0;
        long ans = 0;
        for (long ele : batteries) {
            sum += ele;
        }
        long endTime = sum;
        while (startTime <= endTime) {
            long avgTime = (startTime + endTime) / 2;
            if (isPossibeToRun(n, batteries, avgTime)) {
                ans = avgTime;
                startTime = avgTime + 1;
            } else {
                endTime = avgTime - 1;
            }
        }
        return ans;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).