2002. Maximum Product of the Length of Two Palindromic Subsequences

Problem

Given a string s, find two disjoint palindromic subsequences of s such that the product of their lengths is maximized. The two subsequences are disjoint if they do not both pick a character at the same index.

Return **the *maximum* possible product of the lengths of the two palindromic subsequences**.

A subsequence is a string that can be derived from another string by deleting some or no characters without changing the order of the remaining characters. A string is palindromic if it reads the same forward and backward.

  Example 1:

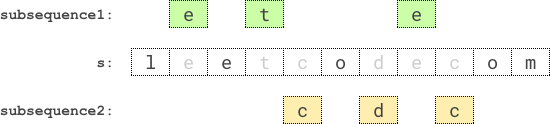
Input: s = "leetcodecom"
Output: 9
Explanation: An optimal solution is to choose "ete" for the 1st subsequence and "cdc" for the 2nd subsequence.
The product of their lengths is: 3 * 3 = 9.

Example 2:

Input: s = "bb"
Output: 1
Explanation: An optimal solution is to choose "b" (the first character) for the 1st subsequence and "b" (the second character) for the 2nd subsequence.
The product of their lengths is: 1 * 1 = 1.

Example 3:

Input: s = "accbcaxxcxx"
Output: 25
Explanation: An optimal solution is to choose "accca" for the 1st subsequence and "xxcxx" for the 2nd subsequence.
The product of their lengths is: 5 * 5 = 25.

  Constraints:

• 2 <= s.length <= 12

• s consists of lowercase English letters only.

Solution (Java)

class Solution {
    public int maxProduct(String s) {
        if (s.length() == 2) {
            return 1;
        }
        List<State> list = new ArrayList<>();
        char[] chars = s.toCharArray();
        Set<State> visited = new HashSet<>();
        for (int i = 0; i < chars.length; ++i) {
            int mask = 1 << i;
            recur(chars, new State(i, i, 0, mask), list, visited);
            recur(chars, new State(i, i + 1, 0, mask), list, visited);
        }
        list.sort((a, b) -> b.cnt - a.cnt);
        int res = 1;
        Set<Integer> explored = new HashSet<>();
        for (int i = 0; i < list.size() - 1; ++i) {
            if (explored.contains(i)) {
                continue;
            }
            State cur = list.get(i);
            if (cur.cnt == 1) {
                break;
            }
            for (int j = i + 1; j < list.size(); ++j) {
                State cand = list.get(j);
                if ((cur.mask & cand.mask) < 1) {
                    if (explored.add(j)) {
                        res = Math.max(res, cur.cnt * cand.cnt);
                    }
                    break;
                }
            }
        }
        return res;
    }

    private void recur(char[] chars, State s, List<State> list, Set<State> visited) {
        if (s.i < 0 || s.j >= chars.length) {
            return;
        }
        if (!visited.add(s)) {
            return;
        }
        if (chars[s.i] == chars[s.j]) {
            int m = s.mask | (1 << s.i) | (1 << s.j);
            int nextCnt = s.cnt + (s.i < s.j ? 2 : 1);
            list.add(new State(s.i, s.j, nextCnt, m));
            recur(chars, new State(s.i - 1, s.j + 1, nextCnt, m), list, visited);
        }
        recur(chars, new State(s.i - 1, s.j, s.cnt, s.mask), list, visited);
        recur(chars, new State(s.i, s.j + 1, s.cnt, s.mask), list, visited);
    }

    private static class State {
        int i;
        int j;
        int cnt;
        int mask;

        public State(int i, int j, int cnt, int mask) {
            this.i = i;
            this.j = j;
            this.cnt = cnt;
            this.mask = mask;
        }

        @Override
        public boolean equals(Object o) {
            if (o == null || o.getClass() != this.getClass()) {
                return false;
            }
            State s = (State) o;
            return this.i == s.i && this.j == s.j && this.mask == s.mask;
        }

        @Override
        public int hashCode() {
            return (this.i * 31 + this.j) * 31 + this.mask;
        }
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).