Maximum Non Negative Product in a Matrix

Problem

You are given a m x n matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.

Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (m - 1, n - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.

Return the **maximum non-negative product *modulo* **10^9 + 7. **If the maximum product is negative, return **-1.

Notice that the modulo is performed after getting the maximum product.

Example 1:

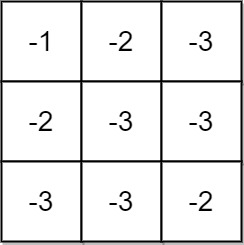
Input: grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
Output: -1
Explanation: It is not possible to get non-negative product in the path from (0, 0) to (2, 2), so return -1.

Example 2:

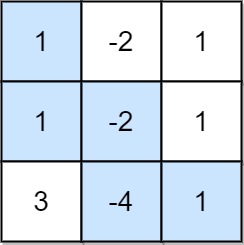
Input: grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
Output: 8
Explanation: Maximum non-negative product is shown (1 * 1 * -2 * -4 * 1 = 8).

Example 3:

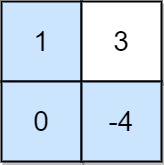
Input: grid = [[1,3],[0,-4]]
Output: 0
Explanation: Maximum non-negative product is shown (1 * 0 * -4 = 0).

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 15
-4 <= grid[i][j] <= 4

Solution (Java)

class Solution {
    private static class Tuple {
        long max;
        long min;

        public Tuple(long a, long b) {
            this.max = a;
            this.min = b;
        }
    }

    public int maxProductPath(int[][] grid) {
        // DP
        if (grid == null || grid.length == 0 || grid[0] == null || grid[0].length == 0) {
            return 0;
        }
        int rows = grid.length;
        int cols = grid[0].length;
        Tuple[][] dp = new Tuple[rows][cols];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                dp[i][j] = new Tuple(1, 1);
            }
        }
        // Init first row and column
        dp[0][0].max = grid[0][0];
        dp[0][0].min = grid[0][0];
        for (int i = 1; i < rows; i++) {
            dp[i][0].max = grid[i][0] * dp[i - 1][0].max;
            dp[i][0].min = grid[i][0] * dp[i - 1][0].min;
        }
        for (int i = 1; i < cols; i++) {
            dp[0][i].max = grid[0][i] * dp[0][i - 1].max;
            dp[0][i].min = grid[0][i] * dp[0][i - 1].min;
        }
        // DP
        for (int i = 1; i < rows; i++) {
            for (int j = 1; j < cols; j++) {
                long up1 = dp[i - 1][j].max * grid[i][j];
                long up2 = dp[i - 1][j].min * grid[i][j];
                long left1 = dp[i][j - 1].max * grid[i][j];
                long left2 = dp[i][j - 1].min * grid[i][j];
                // max(up1, up2, left1, left2)
                dp[i][j].max = Math.max(up1, Math.max(up2, Math.max(left1, left2)));
                // min(up1, up2, left1, left2)
                dp[i][j].min = Math.min(up1, Math.min(up2, Math.min(left1, left2)));
            }
        }
        if (dp[rows - 1][cols - 1].max < 0) {
            return -1;
        }
        return (int) (dp[rows - 1][cols - 1].max % (1e9 + 7));
    }
}

Explain:

nope.

Complexity:

Time complexity : O(n).
Space complexity : O(n).