Problem
A k x k magic square is a k x k grid filled with integers such that every row sum, every column sum, and both diagonal sums are all equal. The integers in the magic square do not have to be distinct. Every 1 x 1 grid is trivially a magic square.
Given an m x n integer grid, return **the *size* (i.e., the side length k) of the largest magic square that can be found within this grid**.
Example 1:
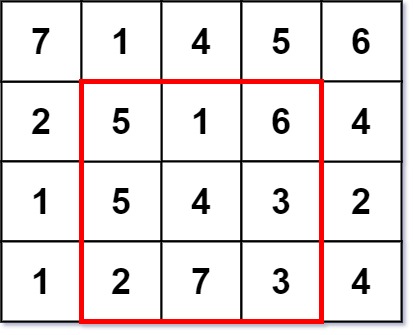
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
Output: 3
Explanation: The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12
Example 2:
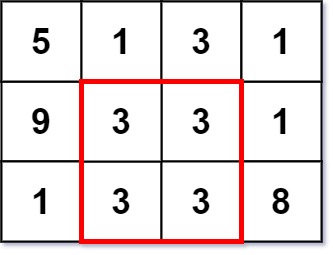
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
Output: 2
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 501 <= grid[i][j] <= 10^6
Solution (Java)
class Solution {
public int largestMagicSquare(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
int[][] rows = new int[m][n + 1];
int[][] cols = new int[m + 1][n];
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
// cumulative sum for each row
rows[i][j + 1] = rows[i][j] + grid[i][j];
// cumulative sum for each column
cols[i + 1][j] = cols[i][j] + grid[i][j];
}
}
// start with the biggest side possible
for (int side = Math.min(m, n); side > 1; side--) {
// check every square
for (int i = 0; i <= m - side; i++) {
for (int j = 0; j <= n - side; j++) {
// checks if a square with top left [i, j] and side length is magic
if (magic(grid, rows, cols, i, j, side)) {
return side;
}
}
}
}
return 1;
}
private boolean magic(int[][] grid, int[][] rows, int[][] cols, int r, int c, int side) {
int sum = rows[r][c + side] - rows[r][c];
int d1 = 0;
int d2 = 0;
for (int k = 0; k < side; k++) {
d1 += grid[r + k][c + k];
d2 += grid[r + side - 1 - k][c + k];
// check each row and column
if (rows[r + k][c + side] - rows[r + k][c] != sum
|| cols[r + side][c + k] - cols[r][c + k] != sum) {
return false;
}
}
// checks both diagonals
return d1 == sum && d2 == sum;
}
}
Explain:
nope.
Complexity:
- Time complexity : O(n).
- Space complexity : O(n).