2536. Increment Submatrices by One

Problem

You are given a positive integer n, indicating that we initially have an n x n 0-indexed integer matrix mat filled with zeroes.

You are also given a 2D integer array query. For each query[i] = [row1i, col1i, row2i, col2i], you should do the following operation:

• Add 1 to every element in the submatrix with the top left corner (row1i, col1i) and the bottom right corner (row2i, col2i). That is, add 1 to mat[x][y] for for all row1i <= x <= row2i and col1i <= y <= col2i.

Return** the matrix** mat** after performing every query.**

  Example 1:

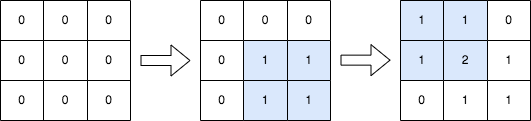
Input: n = 3, queries = [[1,1,2,2],[0,0,1,1]]
Output: [[1,1,0],[1,2,1],[0,1,1]]
Explanation: The diagram above shows the initial matrix, the matrix after the first query, and the matrix after the second query.
- In the first query, we add 1 to every element in the submatrix with the top left corner (1, 1) and bottom right corner (2, 2).
- In the second query, we add 1 to every element in the submatrix with the top left corner (0, 0) and bottom right corner (1, 1).

Example 2:

Input: n = 2, queries = [[0,0,1,1]]
Output: [[1,1],[1,1]]
Explanation: The diagram above shows the initial matrix and the matrix after the first query.
- In the first query we add 1 to every element in the matrix.

  Constraints:

• 1 <= n <= 500

• 1 <= queries.length <= 104

• 0 <= row1i <= row2i < n

• 0 <= col1i <= col2i < n

Solution (Java)

class Solution {
    public int[][] rangeAddQueries(int n, int[][] queries) {
            int[][] mat = new int[n][n];
        for (int[] query : queries) {
            int row1 = query[0], col1 = query[1], row2 = query[2], col2 = query[3];
            for (int i = row1; i <= row2; i++) {
                for (int j = col1; j <= col2; j++) {
                    mat[i][j]++;
                }
            }
        }
        return mat;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).