2661. First Completely Painted Row or Column

Problem

You are given a 0-indexed integer array arr, and an m x n integer matrix mat. arr and mat both contain all the integers in the range [1, m * n].

Go through each index i in arr starting from index 0 and paint the cell in mat containing the integer arr[i].

Return the smallest index i at which either a row or a column will be completely painted in mat.

Example 1:

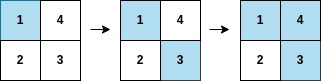
Input: arr = [1,3,4,2], mat = [[1,4],[2,3]]
Output: 2
Explanation: The moves are shown in order, and both the first row and second column of the matrix become fully painted at arr[2].

Example 2:

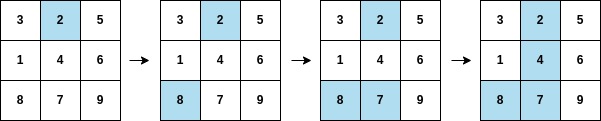
Input: arr = [2,8,7,4,1,3,5,6,9], mat = [[3,2,5],[1,4,6],[8,7,9]]
Output: 3
Explanation: The second column becomes fully painted at arr[3].

Constraints:

• m == mat.length
• n = mat[i].length
• arr.length == m * n
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= arr[i], mat[r][c] <= m * n
• All the integers of arr are unique.
• All the integers of mat are unique.

Solution (Java)

class Solution {
    public int firstCompleteIndex(int[] arr, int[][] mat) {
        Map<Integer,Integer> map = new HashMap();
        for(int i=0; i<arr.length; i++) map.put(arr[i],i);
        int min = arr.length;
//      Row-wise checking
        for(int i=0; i<mat.length; i++){
            int max = 0;
            for(int j=0; j<mat[0].length; j++){
                max = Math.max(max, map.get(mat[i][j]));
            }
            min = Math.min(min,max);
        }
//      Col-wise checking
        for(int i=0; i<mat[0].length; i++){
            int max = 0;
            for(int j=0; j<mat.length; j++){
                max = Math.max(max, map.get(mat[j][i]));
            }
            min = Math.min(min,max);
        }
        return min;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).