2352. Equal Row and Column Pairs

Problem

Given a 0-indexed n x n integer matrix grid, **return the number of pairs *(Ri, Cj)* such that row Ri and column Cj are equal**.

A row and column pair is considered equal if they contain the same elements in the same order (i.e. an equal array).

  Example 1:

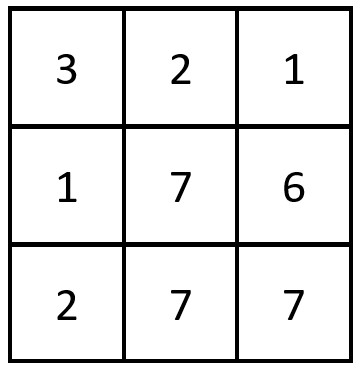
Input: grid = [[3,2,1],[1,7,6],[2,7,7]]
Output: 1
Explanation: There is 1 equal row and column pair:
- (Row 2, Column 1): [2,7,7]

Example 2:

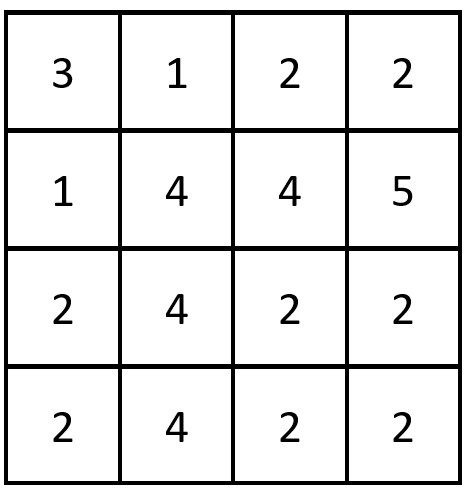
Input: grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
Output: 3
Explanation: There are 3 equal row and column pairs:
- (Row 0, Column 0): [3,1,2,2]
- (Row 2, Column 2): [2,4,2,2]
- (Row 3, Column 2): [2,4,2,2]

  Constraints:

• n == grid.length == grid[i].length

• 1 <= n <= 200

• 1 <= grid[i][j] <= 10^5

Solution (Java)

class Solution {
    public int equalPairs(int[][] grid) {
        int[] tmpCol = new int[grid.length];
        Map<Integer, Integer> pairsMap = new HashMap<>();
        int pairsCounter = 0;
        for (int col = 0; col < grid[0].length; col++) {
            for (int row = 0; row < grid.length; row++) {
                tmpCol[row] = grid[row][col];
            }
            int hashCode = Arrays.hashCode(tmpCol);
            pairsMap.put(hashCode, pairsMap.getOrDefault(hashCode, 0) + 1);
        }
        for (int[] row : grid) {
            int hashCode = Arrays.hashCode(row);
            if (pairsMap.containsKey(hashCode)) {
                pairsCounter += pairsMap.get(hashCode);
            }
        }
        return pairsCounter;
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).