1905. Count Sub Islands

Problem

You are given two m x n binary matrices grid1 and grid2 containing only 0's (representing water) and 1's (representing land). An island is a group of 1's connected 4-directionally (horizontal or vertical). Any cells outside of the grid are considered water cells.

An island in grid2 is considered a **sub-island **if there is an island in grid1 that contains all the cells that make up this island in grid2.

Return the number* of islands in **grid2 **that are considered *sub-islands.

  Example 1:

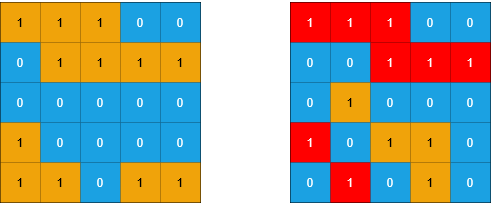
Input: grid1 = [[1,1,1,0,0],[0,1,1,1,1],[0,0,0,0,0],[1,0,0,0,0],[1,1,0,1,1]], grid2 = [[1,1,1,0,0],[0,0,1,1,1],[0,1,0,0,0],[1,0,1,1,0],[0,1,0,1,0]]
Output: 3
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are three sub-islands.

Example 2:

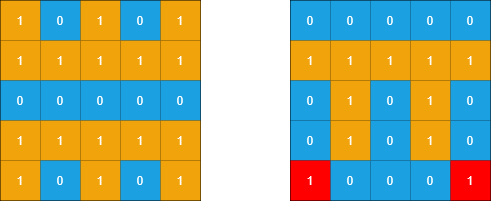
Input: grid1 = [[1,0,1,0,1],[1,1,1,1,1],[0,0,0,0,0],[1,1,1,1,1],[1,0,1,0,1]], grid2 = [[0,0,0,0,0],[1,1,1,1,1],[0,1,0,1,0],[0,1,0,1,0],[1,0,0,0,1]]
Output: 2 
Explanation: In the picture above, the grid on the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered to be part of a sub-island. There are two sub-islands.

  Constraints:

• m == grid1.length == grid2.length

• n == grid1[i].length == grid2[i].length

• 1 <= m, n <= 500

• grid1[i][j] and grid2[i][j] are either 0 or 1.

Solution (Java)

class Solution {
    private int ans = 0;

    public int countSubIslands(int[][] grid1, int[][] grid2) {
        int count = 0;
        for (int i = 0; i < grid2.length; i++) {
            for (int j = 0; j < grid2[0].length; j++) {
                if (grid2[i][j] == 1) {
                    ans = 1;
                    dfs(grid1, grid2, i, j);
                    count += ans;
                }
            }
        }
        return count;
    }

    private void dfs(int[][] grid1, int[][] grid2, int i, int j) {
        if (i < 0 || j < 0 || i >= grid1.length || j >= grid1[0].length || grid2[i][j] == 0) {
            return;
        }
        if (grid1[i][j] == 0) {
            ans = 0;
        }
        grid2[i][j] = 0;
        dfs(grid1, grid2, i - 1, j);
        dfs(grid1, grid2, i + 1, j);
        dfs(grid1, grid2, i, j + 1);
        dfs(grid1, grid2, i, j - 1);
    }
}

Explain:

nope.

Complexity:

• Time complexity : O(n).
• Space complexity : O(n).